Klub 44M - zadania IV 2017»Zadanie 740
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania IV 2017
- Publikacja w Delcie: kwiecień 2017
- Publikacja elektroniczna: 30 marca 2017
- Artykuł źródłowy w wersji do druku [application/pdf]: (71 KB)
-
Zadanie 740 zaproponował pan Witold Bednarek z Łodzi.
Obliczyć kres dolny wartości sumy
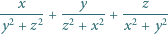
gdy  mogą być dowolnymi liczbami dodatnimi, spełniającymi warunek
mogą być dowolnymi liczbami dodatnimi, spełniającymi warunek 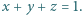

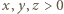 o sumie równej 1. Funkcja
o sumie równej 1. Funkcja 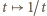 jest wypukła w przedziale
jest wypukła w przedziale 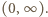 Stosujemy do niej nierówność Jensena dla trójki punktów
Stosujemy do niej nierówność Jensena dla trójki punktów 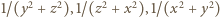 z wagami
z wagami 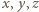 :
: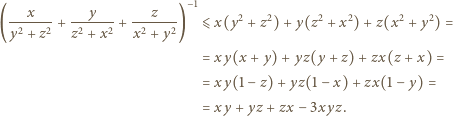
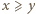 oraz
oraz 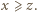 Wówczas
Wówczas 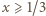 oraz
oraz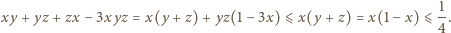
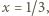 zaś druga - tylko dla
zaś druga - tylko dla 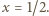 Stąd wniosek, że
Stąd wniosek, że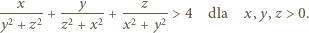
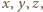 wśród których jedna jest zerem, rozważana suma nadal miałaby sens oraz przyjęłaby wartość 4 dla
wśród których jedna jest zerem, rozważana suma nadal miałaby sens oraz przyjęłaby wartość 4 dla 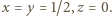 Przy założeniu, że
Przy założeniu, że 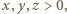 wartość 4 jest (jak widać) nieosiągalna; ale jest granicą badanej sumy np. dla
wartość 4 jest (jak widać) nieosiągalna; ale jest granicą badanej sumy np. dla 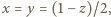 gdy
gdy 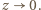 Jest więc jej kresem dolnym.
Jest więc jej kresem dolnym.