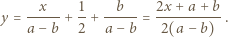Klub 44M - zadania XII 2019»Zadanie 791
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania XII 2019
- Publikacja w Delcie: grudzień 2019
- Publikacja elektroniczna: 30 listopada 2019
- Artykuł źródłowy w wersji do druku [application/pdf]: (374 KB)
Funkcja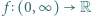 
jest dana wzorem
 |
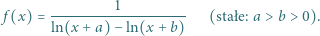Wykazać, że ma ona asymptotę ukośną (przy 
), i znaleźć równanie tej asymptoty.
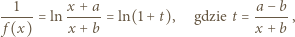
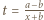dąży do 0, gdy 
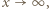zatem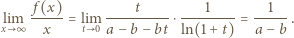
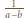; wystarczy zatem, by następująca różnica miała skończoną granicę (przy 
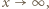czyli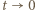 
):
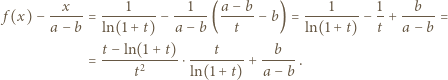
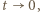pierwszy z ilorazów (w ostatnim uzyskanym wyrażeniu) dąży do granicy 1/2 (bo 
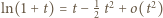). Stąd wniosek, że asymptotą (przy 
) jest prosta o równaniu