Zadanie ZM-1546
o zadaniu...
- Publikacja w Delcie: listopad 2017
- Publikacja elektroniczna: 31 października 2017
Rozważmy ciąg 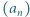 zadany przez
zadany przez 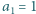 oraz
oraz 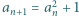 dla
dla 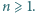 Rozstrzygnąć, czy istnieje dodatnia liczba całkowita
Rozstrzygnąć, czy istnieje dodatnia liczba całkowita 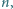 dla której
dla której
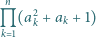
jest kwadratem liczby całkowitej.

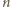 nie istnieje.
nie istnieje.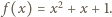 Bezpośrednio sprawdzamy, że dla dowolnego
Bezpośrednio sprawdzamy, że dla dowolnego 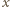 zachodzi równość
zachodzi równość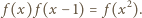
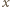 jest dodatnią liczbą całkowitą, to
jest dodatnią liczbą całkowitą, to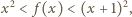
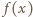 nie jest kwadratem liczby całkowitej.
nie jest kwadratem liczby całkowitej.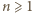 zachodzi równość
zachodzi równość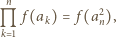
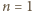 równość
równość 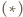 jest spełniona. Przypuśćmy, że zachodzi ona dla pewnego
jest spełniona. Przypuśćmy, że zachodzi ona dla pewnego 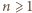 ; wówczas
; wówczas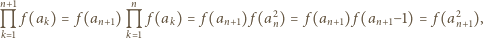
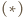 zachodzi również dla
zachodzi również dla 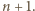 To kończy rozwiązanie.
To kończy rozwiązanie.