Ciąg 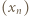 powstaje przez iterowanie funkcji
powstaje przez iterowanie funkcji 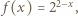 którą będziemy badać na przedziale
którą będziemy badać na przedziale ![[1,2].](/math/temat/matematyka/analiza/zadania/2018/03/25/zm-k44-759/3x-a051a26225a4472d5acd2ead6f6a678d0abff009-im-66,57,43-FF,FF,FF.gif) Ponieważ
Ponieważ 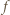 maleje od wartości
maleje od wartości 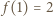 do wartości
do wartości 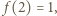 zatem odwzorowuje przedział
zatem odwzorowuje przedział ![[1,2]](/math/temat/matematyka/analiza/zadania/2018/03/25/zm-k44-759/7x-a051a26225a4472d5acd2ead6f6a678d0abff009-im-66,57,43-FF,FF,FF.gif) na siebie i ma w tym przedziale dokładnie jeden punkt stały
na siebie i ma w tym przedziale dokładnie jeden punkt stały 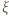 (tj. taki, że
(tj. taki, że 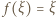 ). Obrazem przedziału
). Obrazem przedziału 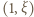 jest przedział
jest przedział 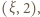 i na odwrót. Stąd wniosek, że wyrazy ciągu
i na odwrót. Stąd wniosek, że wyrazy ciągu 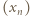 o numerach parzystych należą do jednego z tych przedziałów, a te o nieparzystych - do drugiego.
o numerach parzystych należą do jednego z tych przedziałów, a te o nieparzystych - do drugiego.
Równość 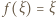 przepisujemy jako
przepisujemy jako 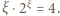 Funkcja
Funkcja 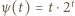 jest rosnąca; przy tym
jest rosnąca; przy tym
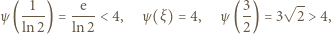
wobec czego
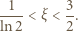 |
(1) |
Ponieważ (z założenia) 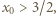 zatem
zatem 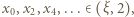 zaś
zaś 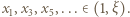
Użyjemy rachunku pochodnych. Oznaczmy (dla krótkości): 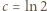 i zauważmy, że
i zauważmy, że 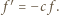 Niech
Niech 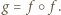 Wówczas
Wówczas
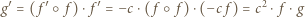
i dalej:
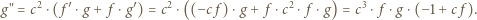 |
(2) |
Dla ![x ∈ [1,ξ]](/math/temat/matematyka/analiza/zadania/2018/03/25/zm-k44-759/1x-ebb224189cbd9ab5aa439f6248ce3382f71c3782-im-66,57,43-FF,FF,FF.gif) mamy nierówność
mamy nierówność 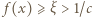 (por. (1)), więc wyrażenie w nawiasie po prawej stronie (2) ma w tych punktach wartość dodatnią. To znaczy, że funkcja
(por. (1)), więc wyrażenie w nawiasie po prawej stronie (2) ma w tych punktach wartość dodatnią. To znaczy, że funkcja 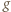 jest ściśle wypukła w przedziale
jest ściśle wypukła w przedziale ![|[1,ξ]](/math/temat/matematyka/analiza/zadania/2018/03/25/zm-k44-759/4x-ebb224189cbd9ab5aa439f6248ce3382f71c3782-im-66,57,43-FF,FF,FF.gif) ; a ponieważ
; a ponieważ 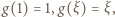 zatem
zatem
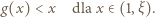 |
(3) |
Ciąg 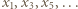 leży w przedziale
leży w przedziale 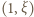 i jest generowany rekurencyjnie wzorem
i jest generowany rekurencyjnie wzorem 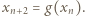 Nierówność (3) pokazuje, że jest to ciąg malejący, i w konsekwencji zbieżny. Jego granica musi być punktem stałym funkcji
Nierówność (3) pokazuje, że jest to ciąg malejący, i w konsekwencji zbieżny. Jego granica musi być punktem stałym funkcji 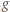 ; jednak nie ma takiego punktu w przedziale otwartym
; jednak nie ma takiego punktu w przedziale otwartym 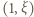 (nierówność (3)). W takim razie granicą tego ciągu musi być liczba 1.
(nierówność (3)). W takim razie granicą tego ciągu musi być liczba 1.
Funkcja ciągła 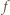 przeprowadza ten ciąg na ciąg rosnący
przeprowadza ten ciąg na ciąg rosnący 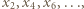 którego granicą jest wobec tego liczba
którego granicą jest wobec tego liczba 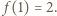 To dowodzi, że niezależnie od wyboru wyrazu początkowego
To dowodzi, że niezależnie od wyboru wyrazu początkowego 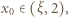 ciąg
ciąg 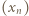 ma podciągi zbieżne do dwóch różnych granic: 1 oraz 2 (i do żadnej innej, bo dowolny podciąg ma nieskończenie wiele wspólnych wyrazów z jednym ze znalezionych podciągów, zbieżnych do 1 lub 2).
ma podciągi zbieżne do dwóch różnych granic: 1 oraz 2 (i do żadnej innej, bo dowolny podciąg ma nieskończenie wiele wspólnych wyrazów z jednym ze znalezionych podciągów, zbieżnych do 1 lub 2).
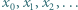 jest określony wzorem rekurencyjnym
jest określony wzorem rekurencyjnym 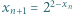 dla
dla 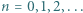 ; wyraz początkowy
; wyraz początkowy 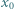 jest dowolną liczbą z przedziału
jest dowolną liczbą z przedziału 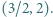 Wyznaczyć wszystkie liczby, będące granicami zbieżnych podciągów ciągu
Wyznaczyć wszystkie liczby, będące granicami zbieżnych podciągów ciągu 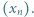

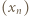 powstaje przez iterowanie funkcji
powstaje przez iterowanie funkcji 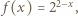 którą będziemy badać na przedziale
którą będziemy badać na przedziale ![[1,2].](/math/temat/matematyka/analiza/zadania/2018/03/25/zm-k44-759/3x-a051a26225a4472d5acd2ead6f6a678d0abff009-im-66,57,43-FF,FF,FF.gif) Ponieważ
Ponieważ 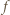 maleje od wartości
maleje od wartości 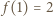 do wartości
do wartości 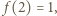 zatem odwzorowuje przedział
zatem odwzorowuje przedział ![[1,2]](/math/temat/matematyka/analiza/zadania/2018/03/25/zm-k44-759/7x-a051a26225a4472d5acd2ead6f6a678d0abff009-im-66,57,43-FF,FF,FF.gif) na siebie i ma w tym przedziale dokładnie jeden punkt stały
na siebie i ma w tym przedziale dokładnie jeden punkt stały 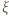 (tj. taki, że
(tj. taki, że 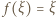 ). Obrazem przedziału
). Obrazem przedziału 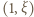 jest przedział
jest przedział 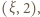 i na odwrót. Stąd wniosek, że wyrazy ciągu
i na odwrót. Stąd wniosek, że wyrazy ciągu 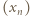 o numerach parzystych należą do jednego z tych przedziałów, a te o nieparzystych - do drugiego.
o numerach parzystych należą do jednego z tych przedziałów, a te o nieparzystych - do drugiego.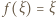 przepisujemy jako
przepisujemy jako 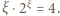 Funkcja
Funkcja 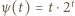 jest rosnąca; przy tym
jest rosnąca; przy tym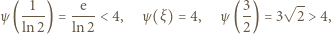
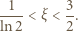
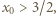 zatem
zatem 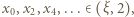 zaś
zaś 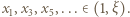
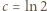 i zauważmy, że
i zauważmy, że 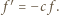 Niech
Niech 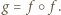 Wówczas
Wówczas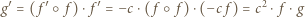
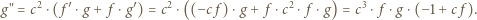
![x ∈ [1,ξ]](/math/temat/matematyka/analiza/zadania/2018/03/25/zm-k44-759/1x-ebb224189cbd9ab5aa439f6248ce3382f71c3782-im-66,57,43-FF,FF,FF.gif) mamy nierówność
mamy nierówność 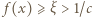 (por. (1)), więc wyrażenie w nawiasie po prawej stronie (2) ma w tych punktach wartość dodatnią. To znaczy, że funkcja
(por. (1)), więc wyrażenie w nawiasie po prawej stronie (2) ma w tych punktach wartość dodatnią. To znaczy, że funkcja 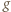 jest ściśle wypukła w przedziale
jest ściśle wypukła w przedziale ![|[1,ξ]](/math/temat/matematyka/analiza/zadania/2018/03/25/zm-k44-759/4x-ebb224189cbd9ab5aa439f6248ce3382f71c3782-im-66,57,43-FF,FF,FF.gif) ; a ponieważ
; a ponieważ 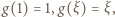 zatem
zatem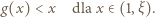
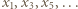 leży w przedziale
leży w przedziale 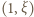 i jest generowany rekurencyjnie wzorem
i jest generowany rekurencyjnie wzorem 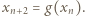 Nierówność (3) pokazuje, że jest to ciąg malejący, i w konsekwencji zbieżny. Jego granica musi być punktem stałym funkcji
Nierówność (3) pokazuje, że jest to ciąg malejący, i w konsekwencji zbieżny. Jego granica musi być punktem stałym funkcji 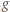 ; jednak nie ma takiego punktu w przedziale otwartym
; jednak nie ma takiego punktu w przedziale otwartym 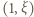 (nierówność (3)). W takim razie granicą tego ciągu musi być liczba 1.
(nierówność (3)). W takim razie granicą tego ciągu musi być liczba 1.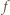 przeprowadza ten ciąg na ciąg rosnący
przeprowadza ten ciąg na ciąg rosnący 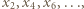 którego granicą jest wobec tego liczba
którego granicą jest wobec tego liczba 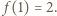 To dowodzi, że niezależnie od wyboru wyrazu początkowego
To dowodzi, że niezależnie od wyboru wyrazu początkowego 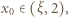 ciąg
ciąg 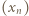 ma podciągi zbieżne do dwóch różnych granic: 1 oraz 2 (i do żadnej innej, bo dowolny podciąg ma nieskończenie wiele wspólnych wyrazów z jednym ze znalezionych podciągów, zbieżnych do 1 lub 2).
ma podciągi zbieżne do dwóch różnych granic: 1 oraz 2 (i do żadnej innej, bo dowolny podciąg ma nieskończenie wiele wspólnych wyrazów z jednym ze znalezionych podciągów, zbieżnych do 1 lub 2).