Klub 44M - zadania V 2015»Zadanie 702
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania V 2015
- Publikacja w Delcie: maj 2015
- Publikacja elektroniczna: 30 kwietnia 2015
- Artykuł źródłowy w wersji do druku [application/pdf]: (76 KB)
-
Zadanie 702 zaproponował pan Piotr Kumor z Olsztyna.
Niech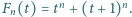 
Udowodnić, że istnieje nieskończenie wiele liczb całkowitych 
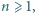dla których równanie 
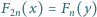nie ma rozwiązań w liczbach całkowitych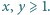 
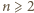Ciekawostka
Auror zadania, pan Piotr Kumor z Olsztyna, opatrzył je komentarzem:
dokładnie przed ćwierćwieczem to samo równanie było przedmiotem zadania ligowego 194 (Delta 5/1990 - treść i rozwiązanie); teza brzmiała: dla 
równanie może mieć w liczbach całkowitych 
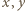co najwyżej skończenie wiele rozwiązań (autor: Marcin Mazur); zaś w rocznym omówieniu (Delta 2/1992) pozostało otwarte pytanie, czy to równanie w ogóle ma rozwiązania poza trywialnymi 
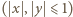; obecna propozycja to mały krok w kierunku próby badania tego problemu.
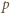jest nieparzystą liczbą pierwszą, równanie 
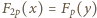nie ma rozwiązań w liczbach całkowitych dodatnich.
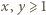jest rozwiązaniem. Zgodnie z małym twierdzeniem Fermata,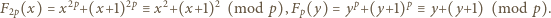
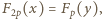to 
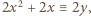czyli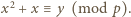 
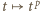(w zbiorze liczb dodatnich) wynika nierówność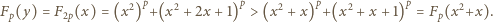
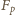jest rosnąca; stąd 
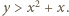Skoro zaś 
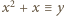(mod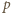 
), widzimy, że 
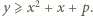A zatem 
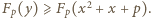Aby uzyskać oczekiwaną sprzeczność, wystarczy wykazać, że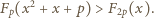
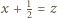; wtedy 
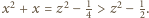Ponownie korzystając z wypukłości funkcji 
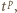mamy nierówność 
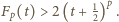Wobec tego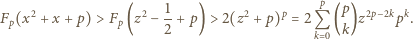
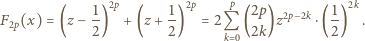
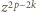jest nie mniejszy niż analogiczny współczynnik w wyrażeniu (3); czyli, że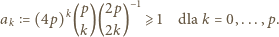
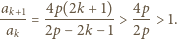
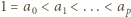; oszacowanie (4) gotowe, dowód zakończony.