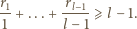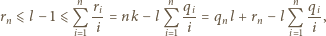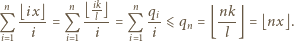Zadanie ZM-1480
o zadaniu...
- Publikacja w Delcie: styczeń 2016
- Publikacja elektroniczna: 01-01-2016
Udowodnić, że dla dowolnej liczby nieujemnej 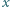 i dowolnej liczby całkowitej dodatniej
i dowolnej liczby całkowitej dodatniej 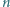 prawdziwa jest nierówność
prawdziwa jest nierówność
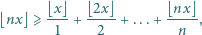
gdzie 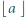 oznacza największą liczbę całkowitą nie większą od
oznacza największą liczbę całkowitą nie większą od 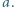

 mamy równość. Ponadto dodanie do dowolnego
mamy równość. Ponadto dodanie do dowolnego 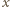 liczby całkowitej
liczby całkowitej 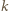 zmienia każdą ze stron nierówności o
zmienia każdą ze stron nierówności o 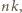 możemy zatem zakładać, że
możemy zatem zakładać, że  należy do przedziału
należy do przedziału 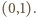 Niech
Niech 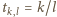 dla takich względnie pierwszych liczb całkowitych dodatnich
dla takich względnie pierwszych liczb całkowitych dodatnich 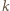 i
i 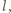 że
że 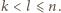 Zauważmy, że obie strony nierówności są w przedziale
Zauważmy, że obie strony nierówności są w przedziale 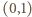 niemalejącymi funkcjami
niemalejącymi funkcjami 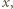 przy czym prawa strona zmienia wartość tylko w punktach
przy czym prawa strona zmienia wartość tylko w punktach 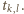 Wystarczy więc sprawdzić nierówność tylko dla tych punktów. Niech od tej pory
Wystarczy więc sprawdzić nierówność tylko dla tych punktów. Niech od tej pory 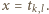
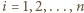 zachodzi równość
zachodzi równość 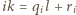 dla pewnych jednoznacznie wyznaczonych liczb całkowitych
dla pewnych jednoznacznie wyznaczonych liczb całkowitych 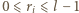 i
i 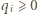 (dzielimy
(dzielimy 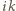 z resztą przez
z resztą przez 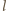 ). Zauważmy, że liczby
). Zauważmy, że liczby 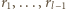 są dodatnie:
są dodatnie: 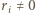 dla
dla 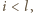 bo inaczej
bo inaczej 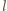 dzieliłoby
dzieliłoby 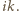 Ponadto te liczby są parami różne - gdy
Ponadto te liczby są parami różne - gdy 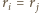 dla
dla 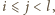 to
to 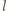 dzieli
dzieli 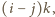 a stąd
a stąd 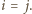 W takim razie ciąg
W takim razie ciąg 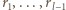 jest pewną permutacją liczb
jest pewną permutacją liczb 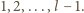 Stąd i z nierówności między średnimi dostajemy
Stąd i z nierówności między średnimi dostajemy