Trójmian kwadratowy»Zadanie 9
o zadaniu...
- Zadanie pochodzi z artykułu Trójmian kwadratowy
- Publikacja w Delcie: październik 2019
- Publikacja elektroniczna: 30 września 2019
- Artykuł źródłowy w wersji do druku [application/pdf]: (388 KB)
Rozważmy trójmiany kwadratowe 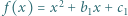 i
i 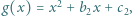 których współczynniki są rzeczywiste i spełniają warunek
których współczynniki są rzeczywiste i spełniają warunek

Dowieść, że trójmiany 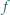 i
i 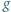 mają obydwa pierwiastki rzeczywiste, a każdy z nich ma jeden pierwiastek leżący na osi liczbowej pomiędzy pierwiastkami drugiego.
mają obydwa pierwiastki rzeczywiste, a każdy z nich ma jeden pierwiastek leżący na osi liczbowej pomiędzy pierwiastkami drugiego.

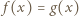 ma dokładnie jedno rozwiązanie
ma dokładnie jedno rozwiązanie 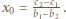 Wówczas
Wówczas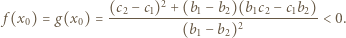
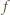 i
i 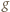 przecinają się tylko w jednym punkcie, leżącym poniżej osi
przecinają się tylko w jednym punkcie, leżącym poniżej osi 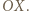 Resztę załatwia własność Darboux.
Resztę załatwia własność Darboux.