Będziemy korzystać - podobnie, jak w rozwiązaniach zadań 654 i 662 (Delta 5/2013, 9/2013) - z twierdzenia Stolza, które mówi, że jeśli 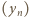 jest ciągiem rosnącym do nieskończoności, wówczas równość
jest ciągiem rosnącym do nieskończoności, wówczas równość
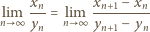 |
(1) |
zachodzi dla każdego ciągu 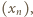 dla którego granica po prawej stronie istnieje. Ponieważ
dla którego granica po prawej stronie istnieje. Ponieważ 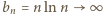 rosnąco, twierdzenie ma szanse zadziałać - warto zająć się ciągiem o wyrazach
rosnąco, twierdzenie ma szanse zadziałać - warto zająć się ciągiem o wyrazach 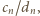 gdzie
gdzie
Jeśli wykażemy, że
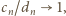
wzór (1) (dla
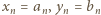
) da wynik
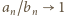
i zakończy rozwiązanie.
Ponownie użyjemy twierdzenia (1) (dla 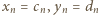 ); ciąg
); ciąg 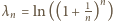 jest rosnący, więc
jest rosnący, więc 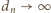 rosnąco. Chcemy dowieść, że liczba 1 jest granicą ciągu o wyrazach
rosnąco. Chcemy dowieść, że liczba 1 jest granicą ciągu o wyrazach
Wszystkie liczby 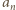 są większe od 1 (oczywista indukcja); ich logarytmy są dodatnie, wobec czego ciąg
są większe od 1 (oczywista indukcja); ich logarytmy są dodatnie, wobec czego ciąg 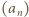 jest rosnący - ma zatem granicę (skończoną lub nie). Granica skończona musiałaby być liczbą
jest rosnący - ma zatem granicę (skończoną lub nie). Granica skończona musiałaby być liczbą 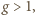 spełniającą równanie
spełniającą równanie 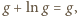 co nie jest możliwe. Tak więc
co nie jest możliwe. Tak więc 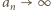 ; co za tym idzie,
; co za tym idzie, 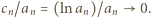 Korzystając ze znanej relacji granicznej
Korzystając ze znanej relacji granicznej 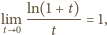 możemy teraz napisać
możemy teraz napisać
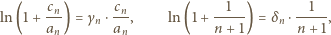
gdzie 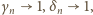 i przepisać wyrażenie (2) w postaci
i przepisać wyrażenie (2) w postaci
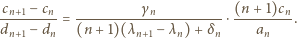 |
(3) |
Z nieco bardziej subtelnej relacji granicznej 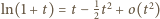 (przy
(przy 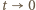 ) możemy wywnioskować, że
) możemy wywnioskować, że
a stąd 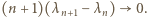 Zatem cały pierwszy czynnik iloczynu po prawej stronie wzoru (3) dąży do 1. Pozostaje dowieść, że drugi czynnik też - czyli że
Zatem cały pierwszy czynnik iloczynu po prawej stronie wzoru (3) dąży do 1. Pozostaje dowieść, że drugi czynnik też - czyli że
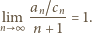 |
(4) |
Jeszcze raz skorzystamy ze wzoru Stolza (1), tym razem biorąc 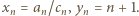 Granica po lewej stronie (4) będzie równa granicy
Granica po lewej stronie (4) będzie równa granicy 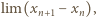 jeśli ta ostatnia istnieje. Skoro
jeśli ta ostatnia istnieje. Skoro
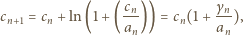
zatem
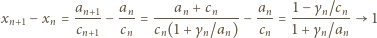
(bo 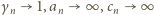 ). To dowodzi słuszności tezy (4), więc i tezy zadania.
). To dowodzi słuszności tezy (4), więc i tezy zadania.
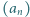 jest określony wzorem rekurencyjnym:
jest określony wzorem rekurencyjnym: 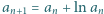 ; wyraz początkowy
; wyraz początkowy 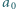 jest dowolną liczbą większą od 1. Udowodnić, że ciąg
jest dowolną liczbą większą od 1. Udowodnić, że ciąg 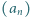 jest asymptotycznie równy ciągowi
jest asymptotycznie równy ciągowi 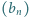 o wyrazach
o wyrazach 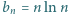 ; to znaczy,
; to znaczy,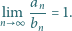

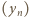 jest ciągiem rosnącym do nieskończoności, wówczas równość
jest ciągiem rosnącym do nieskończoności, wówczas równość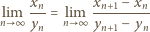
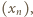 dla którego granica po prawej stronie istnieje. Ponieważ
dla którego granica po prawej stronie istnieje. Ponieważ 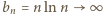 rosnąco, twierdzenie ma szanse zadziałać - warto zająć się ciągiem o wyrazach
rosnąco, twierdzenie ma szanse zadziałać - warto zająć się ciągiem o wyrazach 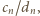 gdzie
gdzie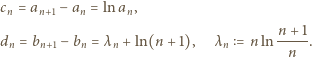
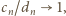 wzór (1) (dla
wzór (1) (dla 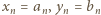 ) da wynik
) da wynik 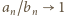 i zakończy rozwiązanie.
i zakończy rozwiązanie.
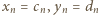 ); ciąg
); ciąg 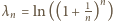 jest rosnący, więc
jest rosnący, więc 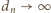 rosnąco. Chcemy dowieść, że liczba 1 jest granicą ciągu o wyrazach
rosnąco. Chcemy dowieść, że liczba 1 jest granicą ciągu o wyrazach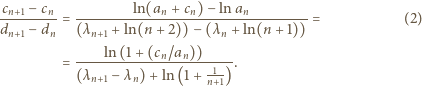
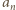 są większe od 1 (oczywista indukcja); ich logarytmy są dodatnie, wobec czego ciąg
są większe od 1 (oczywista indukcja); ich logarytmy są dodatnie, wobec czego ciąg 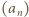 jest rosnący - ma zatem granicę (skończoną lub nie). Granica skończona musiałaby być liczbą
jest rosnący - ma zatem granicę (skończoną lub nie). Granica skończona musiałaby być liczbą 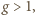 spełniającą równanie
spełniającą równanie 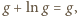 co nie jest możliwe. Tak więc
co nie jest możliwe. Tak więc 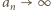 ; co za tym idzie,
; co za tym idzie, 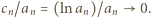 Korzystając ze znanej relacji granicznej
Korzystając ze znanej relacji granicznej 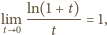 możemy teraz napisać
możemy teraz napisać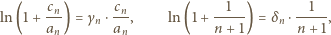
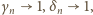 i przepisać wyrażenie (2) w postaci
i przepisać wyrażenie (2) w postaci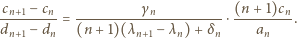
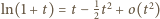 (przy
(przy 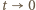 ) możemy wywnioskować, że
) możemy wywnioskować, że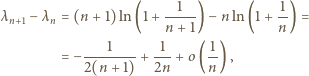
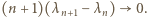 Zatem cały pierwszy czynnik iloczynu po prawej stronie wzoru (3) dąży do 1. Pozostaje dowieść, że drugi czynnik też - czyli że
Zatem cały pierwszy czynnik iloczynu po prawej stronie wzoru (3) dąży do 1. Pozostaje dowieść, że drugi czynnik też - czyli że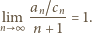
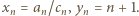 Granica po lewej stronie (4) będzie równa granicy
Granica po lewej stronie (4) będzie równa granicy 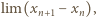 jeśli ta ostatnia istnieje. Skoro
jeśli ta ostatnia istnieje. Skoro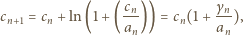
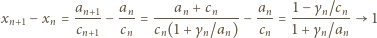
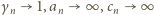 ). To dowodzi słuszności tezy (4), więc i tezy zadania.
). To dowodzi słuszności tezy (4), więc i tezy zadania.