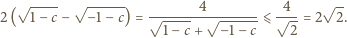Zadanie ZM-1433
o zadaniu...
- Publikacja w Delcie: wrzesień 2014
- Publikacja elektroniczna: 01-09-2014
Określmy funkcję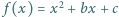 
dla pewnych liczb rzeczywistych 
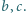Wiadomo, że zbiór 
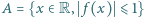jest zbiorem pustym, odcinkiem lub sumą dwóch odcinków (w zależności od wartości 
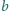i 
). Udowodnić, że za każdym razem łączna długość nie przekracza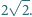 
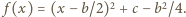Możemy bez utraty ogólności przyjąć więc, że 
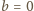(zmiana wartości parametrów na 
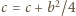oraz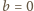 
przesuwa wykres w poziomie, co nie zmienia zbioru 
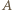). Mamy kilka przypadków.
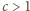; wtedy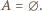 
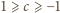; wtedy 
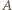jest odcinkiem 
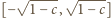o długości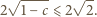 
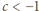; wtedy 
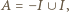gdzie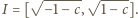 
Łączna długość tych dwóch odcinków wynosi 