Klub 44M - zadania V 2014»Zadanie 682
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania V 2014
- Publikacja w Delcie: maj 2014
- Publikacja elektroniczna: 1 maja 2014
- Artykuł źródłowy w wersji do druku [application/pdf]: (79 KB)
-
Zadanie 682 zaproponował pan Paweł Najman z Krakowa.
Liczby dodatnie 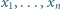 spełniają warunek
spełniają warunek
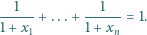
Udowodnić, że
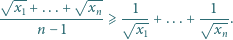

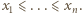 Nierówność daną do udowodnienia przepisujemy w równoważnej postaci
Nierówność daną do udowodnienia przepisujemy w równoważnej postaci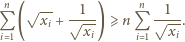
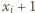 :
: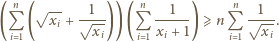
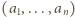 i
i 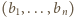 o wyrazach
o wyrazach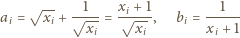
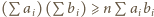 da wówczas dowodzoną tezę
da wówczas dowodzoną tezę 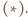
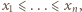 więc ciąg
więc ciąg 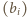 jest nierosnący; chcemy pokazać, że ciąg
jest nierosnący; chcemy pokazać, że ciąg 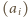 jest niemalejący. Funkcja
jest niemalejący. Funkcja 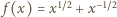 maleje w przedziale
maleje w przedziale 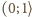 oraz rośnie w przedziale
oraz rośnie w przedziale 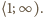 Zatem fragment ciągu
Zatem fragment ciągu 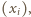 który leży w przedziale
który leży w przedziale 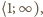 wyznacza niemalejący fragment ciągu o wyrazach
wyznacza niemalejący fragment ciągu o wyrazach 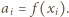 Skoro jednak
Skoro jednak 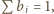 to w przedziale
to w przedziale 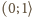 może leżeć co najwyżej jeden wyraz ciągu
może leżeć co najwyżej jeden wyraz ciągu 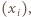 czyli liczba
czyli liczba 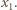 Pozostaje dowieść, że wówczas
Pozostaje dowieść, że wówczas 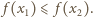 Z założenia
Z założenia 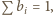 więc
więc 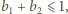 skąd (po prostym przekształceniu)
skąd (po prostym przekształceniu) 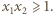 Stąd, ostatecznie,
Stąd, ostatecznie,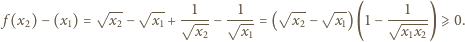
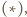 równoważnej z tezą zadania.
równoważnej z tezą zadania.