Klub 44M - zadania II 2020»Zadanie 795
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania II 2020
- Publikacja w Delcie: luty 2020
- Publikacja elektroniczna: 1 lutego 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (496 KB)
Ciąg 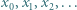 jest określony rekurencyjnie:
jest określony rekurencyjnie: 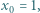
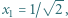
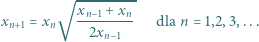 |
Uzasadnić zbieżność i wyznaczyć granicę tego ciągu.

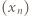 wynika (przez oczywistą indukcję), że wszystkie jego wyrazy są dobrze określonymi liczbami dodatnimi. Weźmy pod uwagę ilorazy
wynika (przez oczywistą indukcję), że wszystkie jego wyrazy są dobrze określonymi liczbami dodatnimi. Weźmy pod uwagę ilorazy 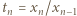 ; ciąg liczb dodatnich
; ciąg liczb dodatnich  z wyrazem początkowym
z wyrazem początkowym 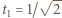 spełnia zależność rekurencyjną
spełnia zależność rekurencyjną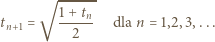
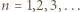 zachodzi równość
zachodzi równość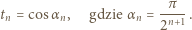
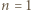 tak jest. Przyjmijmy równość
tak jest. Przyjmijmy równość 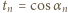 dla pewnego
dla pewnego 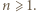 Ponieważ
Ponieważ 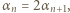 mamy wówczas
mamy wówczas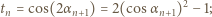
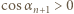 ):
):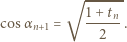
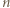 zastąpionym przez
zastąpionym przez 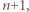 czyli tezę indukcyjną.
czyli tezę indukcyjną.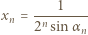
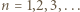 Znów indukcja: dla
Znów indukcja: dla 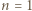 zgadza się (bo
zgadza się (bo 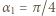 ). Ustalmy
). Ustalmy 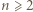 i przyjmijmy słuszność (3) z
i przyjmijmy słuszność (3) z 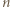 zastąpionym przez
zastąpionym przez 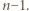 Z takiego założenia indukcyjnego i ze wzoru (2) otrzymujemy
Z takiego założenia indukcyjnego i ze wzoru (2) otrzymujemy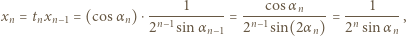
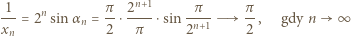
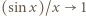 przy
przy 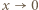 ). Stąd, ostatecznie,
). Stąd, ostatecznie,