Klub 44M - zadania VI 2016»Zadanie 724
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania VI 2016
- Publikacja w Delcie: czerwiec 2016
- Publikacja elektroniczna: 1 czerwca 2016
- Artykuł źródłowy w wersji do druku [application/pdf]: (55 KB)
-
Zadanie 724 zostało opracowane na podstawie propozycji, którą przysłał pan Paweł Najman z Krakowa.
Dowieść, że liczby zespolone 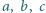 spełniają równanie
spełniają równanie
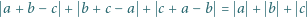
wtedy i tylko wtedy, gdy spełniają równanie
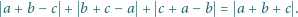

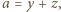
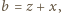
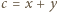 przeprowadza dane dwa równania do postaci
przeprowadza dane dwa równania do postaci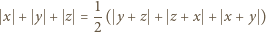
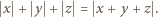
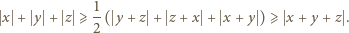
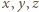 spełniają równanie (2), to spełniają też i równanie (1). Pozostaje do wykazania implikacja przeciwna.
spełniają równanie (2), to spełniają też i równanie (1). Pozostaje do wykazania implikacja przeciwna.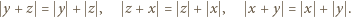
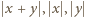 są długościami boków trójkąta (na płaszczyźnie zespolonej) o wierzchołkach
są długościami boków trójkąta (na płaszczyźnie zespolonej) o wierzchołkach 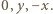 Równość
Równość 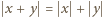 oznacza, że jest on zdegenerowany do odcinka o końcach
oznacza, że jest on zdegenerowany do odcinka o końcach 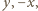 czyli że punkty
czyli że punkty 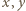 leżą na jednej półprostej, wychodzącej z punktu
leżą na jednej półprostej, wychodzącej z punktu 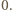 Ta sama konkluzja dla par
Ta sama konkluzja dla par 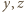 oraz
oraz 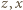 pokazuje, że wszystkie trzy punk
pokazuje, że wszystkie trzy punk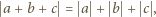
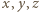 ) równaniu, łączącemu prawe strony (1) i (2). Prosty przykład:
) równaniu, łączącemu prawe strony (1) i (2). Prosty przykład: 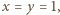
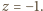 Równania (1) i (2) nie są spełnione, ale ich prawe strony mają jednakową wartość.
Równania (1) i (2) nie są spełnione, ale ich prawe strony mają jednakową wartość.