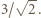Klub 44M - zadania I 2020»Zadanie 794
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania I 2020
- Publikacja w Delcie: styczeń 2020
- Publikacja elektroniczna: 31 grudnia 2019
- Artykuł źródłowy w wersji do druku [application/pdf]: (367 KB)
-
Zadanie 794 zaproponował pan Mikołaj Pater.
Dla liczb rzeczywistych 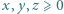 przyjmijmy:
przyjmijmy: 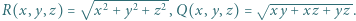 Wyznaczyć najmniejszą możliwą wartość wyrażenia
Wyznaczyć najmniejszą możliwą wartość wyrażenia
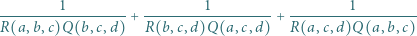 |
dla liczb 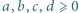 spełniających warunek
spełniających warunek 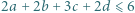 oraz wyznaczyć wszystkie czwórki
oraz wyznaczyć wszystkie czwórki 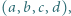 dla których to minimum jest osiągane.
dla których to minimum jest osiągane.

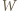 (stale zakładamy, że wszystkie mianowniki są dodatnie). Dwukrotnie stosujemy nierówność między średnimi (po drodze przegrupowując czynniki):
(stale zakładamy, że wszystkie mianowniki są dodatnie). Dwukrotnie stosujemy nierówność między średnimi (po drodze przegrupowując czynniki):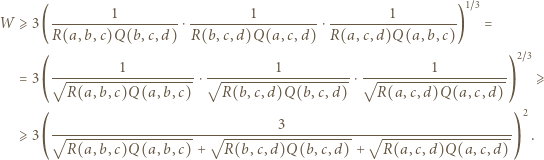
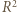 i
i 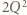 ), dostajemy oszacowanie
), dostajemy oszacowanie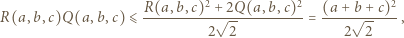
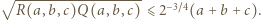 Stąd i z analogicznego oszacowania dla trójek
Stąd i z analogicznego oszacowania dla trójek 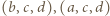 uzyskujemy kontynuację wcześniejszego ciągu nierówności:
uzyskujemy kontynuację wcześniejszego ciągu nierówności: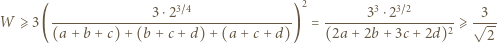
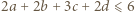 z założenia). Znaleziona wartość zostaje osiągnięta, gdy wszystkie nierówności stają się równościami; więc gdy
z założenia). Znaleziona wartość zostaje osiągnięta, gdy wszystkie nierówności stają się równościami; więc gdy 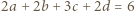 oraz
oraz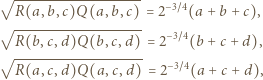
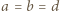 oraz
oraz 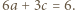 Ponadto - oznaczając krótko
Ponadto - oznaczając krótko 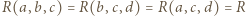 (i podobnie
(i podobnie 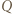 ) - musimy mieć równość
) - musimy mieć równość 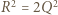 (do takiej pary też była stosowana nierówność między średnimi) - czyli
(do takiej pary też była stosowana nierówność między średnimi) - czyli 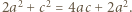 Wraz z równością
Wraz z równością 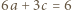 daje to alternatywę:
daje to alternatywę: 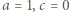 lub
lub 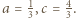 Dla czwórek
Dla czwórek 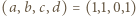 oraz
oraz 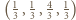 wyznaczone oszacowanie
wyznaczone oszacowanie 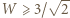 przechodzi w równość. Zatem szukane minimum wynosi
przechodzi w równość. Zatem szukane minimum wynosi