Dla ustalonego, skończonego zbioru punktów na płaszczyźnie wyrażenie
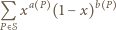
jest wielomianem zmiennej 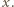 Aby wykazać, że jest to wielomian stale równy
Aby wykazać, że jest to wielomian stale równy 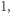 wystarczy sprawdzić, że żądana równość zachodzi dla liczb
wystarczy sprawdzić, że żądana równość zachodzi dla liczb 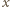 w przedziale
w przedziale 
Rozważmy losowe kolorowanie każdego z danych punktów na biało lub czarno. Załóżmy przy tym, że dowolny punkt malujemy na biało z prawdopodobieństwem 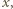 na czarno z prawdopodobieństwem
na czarno z prawdopodobieństwem 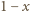 oraz że wszystkie losowania odbywają się niezależnie. Zauważmy, że wówczas dla ustalonego wielokąta
oraz że wszystkie losowania odbywają się niezależnie. Zauważmy, że wówczas dla ustalonego wielokąta 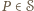 liczba
liczba 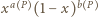 jest prawdopodobieństwem zdarzenia, w którym wszystkie wierzchołki
jest prawdopodobieństwem zdarzenia, w którym wszystkie wierzchołki 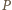 zostały pomalowane na biało, a punkty leżące na zewnątrz
zostały pomalowane na biało, a punkty leżące na zewnątrz 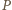 na czarno. Co więcej, dla dwóch różnych wielokątów
na czarno. Co więcej, dla dwóch różnych wielokątów 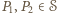 tego typu zdarzenia wykluczają się wzajemnie. Dla dowolnych dwóch różnych wielokątów wypukłych istnieje bowiem wierzchołek jednego z nich, który nie należy do drugiego. Gdyby opisane zdarzenia nie były rozłączne, to wierzchołek ten musiałby być pomalowany na dwa kolory, co jest, oczywiście, niemożliwe.
tego typu zdarzenia wykluczają się wzajemnie. Dla dowolnych dwóch różnych wielokątów wypukłych istnieje bowiem wierzchołek jednego z nich, który nie należy do drugiego. Gdyby opisane zdarzenia nie były rozłączne, to wierzchołek ten musiałby być pomalowany na dwa kolory, co jest, oczywiście, niemożliwe.
Suma
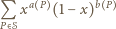
jest w tej sytuacji prawdopodobieństwem zdarzenia, w którym wierzchołki jednego z wielokątów 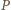 ze zbioru
ze zbioru 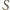 zostały pomalowane na biało, zaś punkty leżące na zewnątrz
zostały pomalowane na biało, zaś punkty leżące na zewnątrz 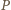 na czarno. Do rozwiązania zadania wystarczy więc stwierdzić, że jest to zdarzenie pewne - co oznacza, że w dowolnym pokolorowaniu taki wielokąt istnieje.
na czarno. Do rozwiązania zadania wystarczy więc stwierdzić, że jest to zdarzenie pewne - co oznacza, że w dowolnym pokolorowaniu taki wielokąt istnieje.
Szukanym wielokątem jest wielokąt 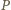 będący otoczką wypukłą białych punktów - czyli najmniejszym wielokątem wypukłym, który zawiera punkty białe (w przypadku gdy liczba punktów białych jest równa
będący otoczką wypukłą białych punktów - czyli najmniejszym wielokątem wypukłym, który zawiera punkty białe (w przypadku gdy liczba punktów białych jest równa 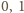 lub
lub 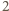 ich otoczką wypukłą jest odpowiednio zbiór pusty, punkt i odcinek). Jego wierzchołki są koloru białego, a każdy inny punkt biały znajduje się w jego wnętrzu.
ich otoczką wypukłą jest odpowiednio zbiór pusty, punkt i odcinek). Jego wierzchołki są koloru białego, a każdy inny punkt biały znajduje się w jego wnętrzu.
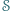 oznacza zbiór wszystkich wielokątów wypukłych o wierzchołkach w tym zbiorze (jako wielokąty wypukłe traktujemy również zbiór pusty, pojedyncze punkty oraz odcinki). Dla dowolnego wielokąta
oznacza zbiór wszystkich wielokątów wypukłych o wierzchołkach w tym zbiorze (jako wielokąty wypukłe traktujemy również zbiór pusty, pojedyncze punkty oraz odcinki). Dla dowolnego wielokąta 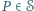 przez
przez 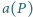 i
i 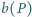 oznaczamy odpowiednio liczbę punktów z danego zbioru, które leżą na obwodzie i na zewnątrz wielokąta
oznaczamy odpowiednio liczbę punktów z danego zbioru, które leżą na obwodzie i na zewnątrz wielokąta 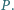 Wykazać, że dla każdej liczby rzeczywistej
Wykazać, że dla każdej liczby rzeczywistej  zachodzi równość
zachodzi równość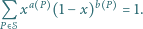

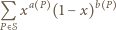
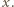 Aby wykazać, że jest to wielomian stale równy
Aby wykazać, że jest to wielomian stale równy 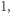 wystarczy sprawdzić, że żądana równość zachodzi dla liczb
wystarczy sprawdzić, że żądana równość zachodzi dla liczb 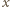 w przedziale
w przedziale 
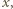 na czarno z prawdopodobieństwem
na czarno z prawdopodobieństwem 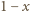 oraz że wszystkie losowania odbywają się niezależnie. Zauważmy, że wówczas dla ustalonego wielokąta
oraz że wszystkie losowania odbywają się niezależnie. Zauważmy, że wówczas dla ustalonego wielokąta 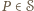 liczba
liczba 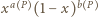 jest prawdopodobieństwem zdarzenia, w którym wszystkie wierzchołki
jest prawdopodobieństwem zdarzenia, w którym wszystkie wierzchołki 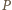 zostały pomalowane na biało, a punkty leżące na zewnątrz
zostały pomalowane na biało, a punkty leżące na zewnątrz 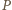 na czarno. Co więcej, dla dwóch różnych wielokątów
na czarno. Co więcej, dla dwóch różnych wielokątów 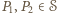 tego typu zdarzenia wykluczają się wzajemnie. Dla dowolnych dwóch różnych wielokątów wypukłych istnieje bowiem wierzchołek jednego z nich, który nie należy do drugiego. Gdyby opisane zdarzenia nie były rozłączne, to wierzchołek ten musiałby być pomalowany na dwa kolory, co jest, oczywiście, niemożliwe.
tego typu zdarzenia wykluczają się wzajemnie. Dla dowolnych dwóch różnych wielokątów wypukłych istnieje bowiem wierzchołek jednego z nich, który nie należy do drugiego. Gdyby opisane zdarzenia nie były rozłączne, to wierzchołek ten musiałby być pomalowany na dwa kolory, co jest, oczywiście, niemożliwe.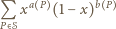
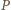 ze zbioru
ze zbioru 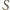 zostały pomalowane na biało, zaś punkty leżące na zewnątrz
zostały pomalowane na biało, zaś punkty leżące na zewnątrz 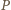 na czarno. Do rozwiązania zadania wystarczy więc stwierdzić, że jest to zdarzenie pewne - co oznacza, że w dowolnym pokolorowaniu taki wielokąt istnieje.
na czarno. Do rozwiązania zadania wystarczy więc stwierdzić, że jest to zdarzenie pewne - co oznacza, że w dowolnym pokolorowaniu taki wielokąt istnieje.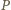 będący otoczką wypukłą białych punktów - czyli najmniejszym wielokątem wypukłym, który zawiera punkty białe (w przypadku gdy liczba punktów białych jest równa
będący otoczką wypukłą białych punktów - czyli najmniejszym wielokątem wypukłym, który zawiera punkty białe (w przypadku gdy liczba punktów białych jest równa 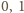 lub
lub 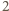 ich otoczką wypukłą jest odpowiednio zbiór pusty, punkt i odcinek). Jego wierzchołki są koloru białego, a każdy inny punkt biały znajduje się w jego wnętrzu.
ich otoczką wypukłą jest odpowiednio zbiór pusty, punkt i odcinek). Jego wierzchołki są koloru białego, a każdy inny punkt biały znajduje się w jego wnętrzu.