Klub 44M - zadania II 2017»Zadanie 728
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania II 2017
- Publikacja w Delcie: luty 2017
- Publikacja elektroniczna: 31 stycznia 2017
- Artykuł źródłowy w wersji do druku [application/pdf]: (155 KB)
-
Zadanie 728 zaproponował pan Witold Bednarek z Łodzi
Czy istnieje funkcja różniczkowalna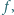 
będąca różnowartościowym odwzorowaniem zbioru wszystkich liczb dodatnich na ten sam zbiór, i taka, że jej pochodna jest funkcją odwrotną do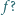 
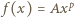(motywacja: zarówno pochodna, jak i funkcja odwrotna do takiej funkcji, też ma taką postać - próba ma szansę powodzenia). Gdy stałe 
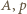są dodatnie, funkcja 
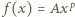jest ściśle rosnąca i przekształca przedział 
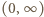na ten sam przedział. Dla ustalonej wartości 
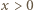rozwiązujemy równanie 
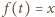(z niewiadomą 
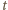), otrzymując 
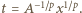Tak więc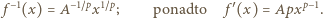
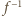i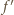 
były identyczne, wystarczy, by parametry dodatnie 
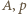spełniały równania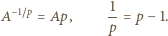
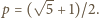Dla tej stałej 
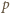pierwsze równanie przybiera formę 
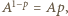z rozwiązaniem 
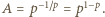Funkcja 
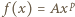z tymi parametrami ma wymaganą własność.