Dyskretny Darboux»Zadanie 3
o zadaniu...
- Zadanie pochodzi z artykułu Dyskretny Darboux
- Publikacja w Delcie: maj 2020
- Publikacja elektroniczna: 30 kwietnia 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (365 KB)
Nauczyciel napisał na tablicy trójmian kwadratowy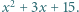 
Następnie wszyscy uczniowie w klasie podchodzili kolejno do tablicy; każdy z nich zmniejszał albo zwiększał o jeden współczynnik przy 
albo wyraz wolny trójmianu. Na koniec okazało się, że na tablicy widnieje trójmian 
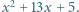Udowodnić, że w pewnym momencie na tablicy był napisany trójmian o pierwiastkach całkowitych.
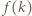będzie wartością danego trójmianu w punkcie 
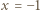po zmianie współczynników przez 
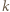-tego ucznia i niech 
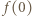będzie wartością w -1 trójmianu napisanego przez nauczyciela. Zauważmy, że 
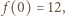a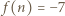 
(gdzie 
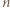to numer ostatniego ucznia). Ponadto zachodzi nierówność 
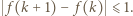Rzeczywiście - jest to jasne, gdy zmieniamy wyraz wolny, zaś zmieniając o 
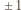wartość współczynnika przy 
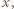dodajemy lub odejmujemy 1 do wartości wielomianu w -1. W takim razie istnieje takie 
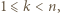że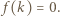 
Zatem w pewnym momencie na tablicy był napisany trójmian 
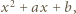którego jednym z pierwiastków było -1; ze wzorów Viète'a wnosimy, że drugim jego pierwiastkiem była liczba całkowita 