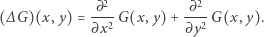Czy można usłyszeć kształt bębenka?

Każdy, komu choć raz zdarzyło się grać na gitarze lub innym instrumencie strunowym, dobrze wie, że na wysokość dźwięku ma wpływ między innymi długość struny. Uderzając w struny zbudowane z tego samego materiału i o tych samych grubościach, lecz o różnych długościach, otrzymamy dwie różne częstotliwości drgań, a więc dwa dźwięki o różnych wysokościach. A jak to jest z instrumentami perkusyjnymi? Czy na podstawie brzmienia drgającej membrany bębenka można powiedzieć coś o jego kształcie?

Jedne z pierwszych prób odpowiedzi na to pytanie pochodzą od Marka Kaca. Żeby przybliżyć tematykę, jaką się zajmował, należy przyjrzeć się opisanemu zagadnieniu z perspektywy analizy matematycznej.

Przez 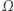$Ω$ będę oznaczała otwarty, spójny podzbiór 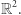$2 |R .$ Jest to model naszej membrany, która pod wpływem uderzenia będzie się odchylała. Aby móc ściśle odpowiedzieć na tytułowe pytanie, najpierw musimy matematycznie sformalizować "brzmienie bębenka". Niestety, w tym artykule nie mamy miejsca na dokładną analizę fizycznego modelu drgania membrany. Wynika z niego jednak, że od strony matematycznej brzmienie jest zdefiniowane przez pewien zbiór zwany widmem drgań i oznaczany przez 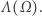$(Ω |Λ$ Jest to zbiór wartości 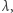$λ,$ dla których istnieje taka niezerowa funkcja 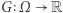$Ω G$ (określająca amplitudę drgań w różnych punktach membrany), że

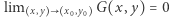$(x,y)=0 |lim x,y x0,y0 G$ dla dowolnego punktu 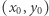$(x0,y0)$ leżącego na brzegu 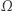$Ω$ (odpowiada to założeniu, że brzeg membrany jest nieruchomy; założenie to nazywa się warunkiem brzegowym Dirichleta),
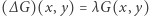$)(x,y)=λG(x,y) (∆ G$ dla wszystkich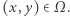 $|(x,y) ∈Ω$

Symbolem 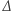$|∆$ oznaczamy laplasjan, czyli pewien operator, który z jednych funkcji tworzy inne (podobnie jak np. operator różniczkowania 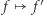$f ( f ′$ ). Czytelników zaznajomionych z cząstkowymi pochodnymi odsyłamy do definicji na marginesie. Do zrozumienia najistotniejszej części tego artykułu wystarcza jednak elementarna wiedza z geometrii oraz przyjęcie do wiadomości, że laplasjan jest

addytywny: $+H+∆H), |∆(G$
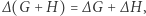
niezmienniczy ze względu na izometrie: jeśli 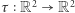$R2 τ R2$ jest izometrią, to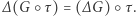 $○τ)=(∆G)○τ. ∆ (G$

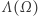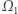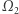Fizycznie widmo drgań $(Ω Λ$ jest zbiorem częstotliwości, z jakimi może drgać uderzona membrana. Jeśli zatem udałoby się nam znaleźć dwie membrany o różnych kształtach (tj. dwa nieizometryczne obszary $Ω$ i $|Ω$ ) i tym samym widmie drgań, otrzymalibyśmy negatywną odpowiedź na tytułowe pytanie. Właśnie w tej formie było ono zadane w 1966 roku przez Marka Kaca w jego artykule "Can one hear the shape of a drum?". Okazuje się, że odpowiedź faktycznie jest negatywna - istnieje już wiele przykładów, które potwierdzają, że nie da się usłyszeć kształtu bębenka. Pierwsze z nich były dosyć skomplikowane (jak na przykład konstrukcja Johna Milnora z 1964 roku: dwa nieprzystające 16-wymiarowe torusy o tym samym widmie drgań - z rozmaitych przyczyn nikt nie produkuje tego rodzaju bębenków...). Obecnie istnieją już konstrukcje dużo prostsze. Ta, którą przytoczymy, została podana w 1992 roku przez Carolyn Gordon, Davida L. Webba oraz Scotta Wolperta w artykule "One cannot hear the shape of a drum".

Cały artykuł dostępny jest w wersji do druku: (527 KB)