Klub 44M - zadania III 2014»Zadanie 677
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania III 2014
- Publikacja w Delcie: marzec 2014
- Publikacja elektroniczna: 2 marca 2014
- Artykuł źródłowy w wersji do druku [application/pdf]: (57 KB)
Rozważamy trójki liczb rzeczywistych
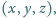 spełniające
warunki
spełniające
warunki
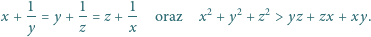 |
Wyznaczyć wszystkie możliwe wartości iloczynu
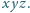

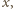
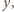
 muszą być różne od zera. Przepisujemy
pierwsze równanie jako
muszą być różne od zera. Przepisujemy
pierwsze równanie jako
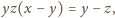 i dalej (cyklicznie)
i dalej (cyklicznie)
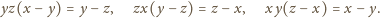
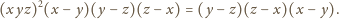
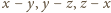 była zerem, to wobec
zależności (1) wszystkie byłyby zerami, czyli liczby
była zerem, to wobec
zależności (1) wszystkie byłyby zerami, czyli liczby
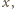
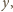
 byłyby równe. To się jednak kłóci z nierównością, daną
w założeniach. Różnice te są więc różne od zera. Równanie (2) po
skróceniu daje wynik:
byłyby równe. To się jednak kłóci z nierównością, daną
w założeniach. Różnice te są więc różne od zera. Równanie (2) po
skróceniu daje wynik:
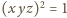 ; jedynymi możliwymi wartościami
iloczynu
; jedynymi możliwymi wartościami
iloczynu
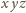 są liczby
są liczby
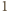 oraz
oraz
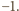 Każda z nich jest
faktycznie osiągalna – na przykład dla
Każda z nich jest
faktycznie osiągalna – na przykład dla
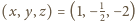 oraz
oraz