Co, że to nie zawsze działa? No faktycznie, można podać bardzo proste zdania, które są prawdziwe tylko dla początkowych paru liczb, a potem przestają być prawdziwe. Najprostsze zdania to "twierdzenia" typu każda liczba naturalna jest mniejsza od miliona. Faktycznie, gdy sprawdzimy prawdziwość takiego zdania dla 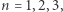dostajemy zdania prawdziwe. Nawet dla 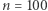jest to prawda. No ale - tu wszyscy się uśmiechamy - nawet małe dziecko wie, że w oczywisty sposób to stwierdzenie nie jest prawdziwe dla, na przykład,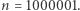

Jednak gdy wzór jest nieco bardziej zagmatwany, możemy dać się ponieść fałszywej intuicji, że skoro nieoczywisty fakt zaskakuje nas dla niewielkich wartości początkowych, to będzie tak zawsze. Różni matematycy ulegali takim mirażom. Jednym z nich był wielki Pierre de Fermat, który sądził, że liczby postaci 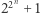są pierwsze dla każdego 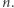Faktycznie, podstawiając 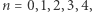dostajemy liczby 3, 5, 17, 257, 65 537 - wszystkie one są pierwsze. Jednak, co wykrył Euler nieco później, już piąta liczba Fermata równa 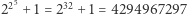może zostać przedstawiona w postaci iloczynu 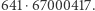Metoda, której użył Euler, bazowała na pewnym fakcie znanym też Fermatowi; historycy zastanawiają się, czemu Fermat tego nie zauważył. Podejrzewa się, że mógł po prostu pomylić się w obliczeniach.

Znalezienie rozkładu szóstej liczby Fermata, czyli 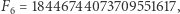było już poza zasięgiem uczonych niedysponujących komputerami, ale dziś wiadomo, że jest to liczba złożona i mniejszy z jej dwóch dzielników to 274 177. Za pomocą komputerów znaleziono również rozkłady liczb 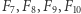i 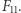Wiadomo też, że liczby Fermata o numerach od 12 do 30 są złożone. Co dalej - nie wiadomo, to znaczy nie wiadomo, czy są jakieś pierwsze liczby Fermata inne niż pięć początkowych i czy trzydziesta pierwsza lub któraś z dalszych liczb Fermata jest złożona.

Podział koła cięciwami

Jedną z metod odkrywania faktów o liczbach naturalnych jest obserwacja małych przypadków, postawienie hipotezy, zbadanie jej prawdziwości dla małych wartości, a następnie próba uogólnienia i, jeśli się da, udowodnienie - zazwyczaj przez indukcję - ogólnego wzoru. Spróbujmy zmierzyć się z takim oto zadaniem. Wybierzmy punktów na brzegu koła i połączmy każdy z każdym. Na ile maksymalnie części dzielą koło wszystkie tak poprowadzone cięciwy? Widać, że aby nie zmarnować żadnego możliwego do uzyskania obszaru, wybrane punkty nie powinny być ułożone zbyt regularnie: żadne trzy cięciwy nie powinny się przecinać w tym samym punkcie. Zbadajmy parę początkowych wartości. Dla jednego punktu mamy 1 obszar - zero cięciw i całe koło. Dwa punkty tworzą jedną cięciwę i dwa obszary, trzy generują z cięciw trójkąt dzielący koło na 4 obszary. Cztery punkty dają nam 8 obszarów, pięć punktów 16 obszarów... No to już widzimy wzór: maksymalna liczba obszarów dla 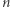punktów to po prostu 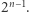Sprawdzamy jeszcze dla i bęc! Okazuje się, że nie da się wykroić 32 obszarów. Najwyżej 31.

Niestety nasz wzór jest błędny: nie uda się nam krok indukcyjny. Trzeba by pokazać, że nowy punkt zwiększa dwukrotnie liczbę obszarów, a dla większych jest to niemożliwe. W rzeczywistości wzór na maksymalną liczbę obszarów to 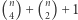albo, jak kto woli, 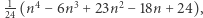co przez przypadek dla pierwszych 5 wartości daje kolejne potęgi dwójki, ale potem już niekoniecznie (początkowe wartości to ).

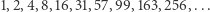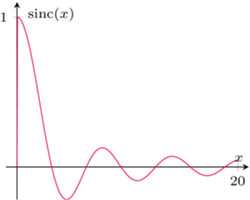
Teraz trochę bardziej zaawansowany przykład, ale robiący wrażenie. Wiąże się on z funkcją 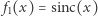(łac. sinus cardinalis), którą definiuje się następująco:

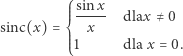Przyjrzyjmy się wykresowi tej funkcji. Widać, że z grubsza to, co jest nad osią 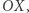przeważa nad tym, co jest pod nią. Innymi słowy, łączne pole między krzywą wykresu a osią 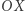nad tą osią jest większe od łącznego pola pod osią. Pola kolejnych fragmentów nad i pod osią dość szybko zanikają, a różnica sum tych pól dąży do pewnej wartości rzeczywistej. Jest to całka oznaczona 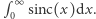Całka ta jest dość paskudna - funkcja 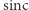nie ma elementarnej funkcji pierwotnej, ale można wyznaczyć wartość tej całki oznaczonej na całej dodatniej półosi. Jest ona równa dokładnie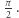

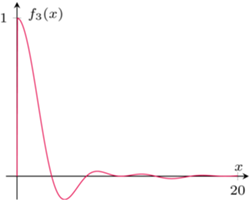
Takie rzeczy się zdarzają. Jednak naprawdę ciekawie się robi, gdy nieco zmodyfikujemy funkcję podcałkową. Rozważmy funkcję 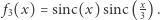Jej wykres przypomina wykres funkcji 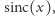a całka 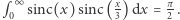Rozważmy jeszcze funkcję 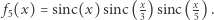Jej całka na dodatniej półosi też wynosi dokładnie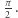

Co dalej? Skoro tak dobrze nam idzie, to spróbujmy obliczyć całki z iloczynów kolejnych funkcji sinc z argumentami będącymi kolejnymi nieparzystymi ułamkami 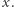Zatem mamy

No to już chyba nic złego się nie może stać. Tymczasem okazuje się, że

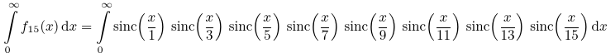
wcale nie jest równe tylko 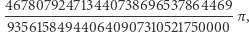co jest prawie dokładnie równe 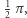ale nie do końca. Ułamek, który stoi przed 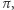ma w przybliżeniu wartość równą 0,499999999992646, więc różni się od 0,5 o niespełna jedną stumiliardową.

Nie muszę dodawać, że 13 jest ostatnią liczbą nieparzystą, dla której całka z iloczynu funkcji sinc z nieparzystymi mianownikami pod jest dokładnie równa Potem ta cudowna własność zanika i dla każdej większej liczby nieparzystej całka ta już jest mniejsza od 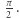Co tu się dzieje?

Na ten fenomen wpadła dwójka matematyków kanadyjskich: David i Jonathan Borweinowie (ojciec i syn). W 2001 roku opublikowali pracę, która zszokowała wielu matematyków. Od tej pory całki omawianej postaci nazywane są całkami Borweinów (Borwein integrals). Jest sporo prac wyjaśniających przyczyny tej niezwykłej anomalii; żadna z nich nie odnosi się do pechowości liczby 13. W oryginalnej pracy autorzy piszą nawet, że podczas weryfikacji tego wyniku dla 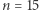sprawdzający go za pomocą komputera był przekonany o błędzie oprogramowania. Trudno się dziwić.

Najprościej można objaśnić moment załamania regularności, odnosząc się do transformat Fouriera i operatora konwolucji, co jednak wykracza poza zakres tego artykułu. Dla zainteresowanych polecam pracę H. Schmida Two curious integrals and a graphic proof. W skrócie, kluczową własnością trzynastki jest to, że jest to ostatnia nieparzysta liczba, dla której suma odwrotności kolejnych nieprzekraczających jej liczb nieparzystych (z pominięciem 1) nie przekracza jedynki. Po prostu 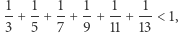ale po dodaniu 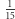przekraczamy jedynkę. Co nam ta jedynka wadzi na drodze do uzyskania 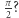Tu niestety trzeba się odnieść do konwolucji - ja nie potrafię tego inaczej wytłumaczyć. Jednak za pomocą tego mechanizmu można się bawić w jeszcze bardziej szokujące wyniki. Na przykład całki

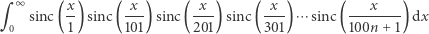będą równe 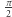tak długo, jak długo szereg ułamków 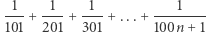nie przekroczy jedynki, a potem dla większych 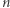już zawsze będą od 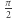mniejsze. Dla jakiego 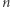to się stanie? Dla bardzo dużego. Naprawdę, bardzo. Chętnych zweryfikować ten rezultat własnoręcznie i sprawdzić, ile wyrazów tego szeregu czyni jego sumę większą od jedynki, śpieszę ostrzec, że na pewno prosta metoda polegająca na sumowaniu ułamków aż się minie jedynkę nie zadziała - po prostu nie doczekamy się wyników. Otóż najmniejszym 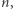dla którego ta całka będzie mniejsza od 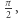jest 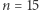341 178 777 673 149 429 167 740 440 969 249 338 310 889. Czyli początkowych 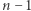całek będzie dokładnie równych 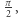a potem już żadna. No to teraz, zdolni informatycy, pytanie: jak można taką wartość tak dokładnie wyznaczyć? To samo w sobie jest bardzo ciekawym zadaniem. Więc nawet zachęcam tych, którzy mają dostęp do komputera i umieją programować, aby spróbowali wyznaczyć to graniczne 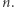Ostrzegam: nie jest to proste zadanie.