O nierównościach typu Diananda–Shapiro
Zacznijmy od przypomnienia zadania 766 z Klubu 44M (Delta 9/2018)...
Powyższy problem można w naturalny sposób sformułować w ogólniejszej postaci. Niech 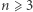 będzie liczbą całkowitą oraz
będzie liczbą całkowitą oraz 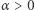 liczbą rzeczywistą. Oznaczmy przez
liczbą rzeczywistą. Oznaczmy przez 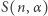 największe ograniczenie dolne wartości sumy
największe ograniczenie dolne wartości sumy
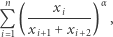 |
gdzie 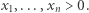 Wówczas zadanie 766 to pytanie o jak najlepsze oszacowanie
Wówczas zadanie 766 to pytanie o jak najlepsze oszacowanie 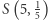 z dołu. Co wiadomo w tej kwestii dla ogólnych wartości
z dołu. Co wiadomo w tej kwestii dla ogólnych wartości  i
i 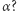
Dla 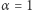 zagadnienie jest znane jako problem Shapiro. Ma on długą i barwną historię, która rozpoczęła się od zadania zaproponowanego przez Joela Shapiro w 1954 roku na łamach The American Mathematical Monthly, w którym prosił on czytelników magazynu o udowodnienie, że
zagadnienie jest znane jako problem Shapiro. Ma on długą i barwną historię, która rozpoczęła się od zadania zaproponowanego przez Joela Shapiro w 1954 roku na łamach The American Mathematical Monthly, w którym prosił on czytelników magazynu o udowodnienie, że 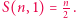 Okazało się, że zależność ta nie jest prawdziwa; pierwszy kontrprzykład
Okazało się, że zależność ta nie jest prawdziwa; pierwszy kontrprzykład 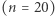 pojawił się w 1956 roku (James Lighthill), w 1985 roku B.A. Troesch zaproponował elegancki kontrprzykład dla
pojawił się w 1956 roku (James Lighthill), w 1985 roku B.A. Troesch zaproponował elegancki kontrprzykład dla 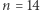 - należy rozważyć ciąg liczb
- należy rozważyć ciąg liczb 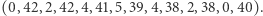 Okazuje się, że jest to najmniejszy (co do
Okazuje się, że jest to najmniejszy (co do  ) możliwy kontrprzykład - hipoteza Shapiro została udowodniona dla parzystych
) możliwy kontrprzykład - hipoteza Shapiro została udowodniona dla parzystych 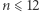 oraz nieparzystych
oraz nieparzystych 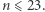 Wiadomo również, jaka jest największa stała
Wiadomo również, jaka jest największa stała 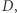 dla której
dla której 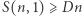 dla wszystkich
dla wszystkich 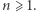 Jest to tak zwana stała Drinfelda i wynosi w przybliżeniu
Jest to tak zwana stała Drinfelda i wynosi w przybliżeniu 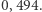 Precyzyjniej,
Precyzyjniej, 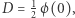 gdzie
gdzie 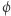 jest największą funkcją wypukłą, która ogranicza z dołu funkcje
jest największą funkcją wypukłą, która ogranicza z dołu funkcje 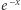 oraz
oraz 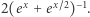 Zatem dla
Zatem dla 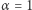 znamy kompletną odpowiedź. Szczegóły znajdziemy na przykład w [1] i [2]. Warto przy okazji nadmienić, że Władimir Drinfeld - autor wspomnianej nierówności - był laureatem Medalu Fieldsa w 1990 roku, a niedawno (w 2018 roku) otrzymał Nagrodę Wolfa w dziedzinie matematyki.
znamy kompletną odpowiedź. Szczegóły znajdziemy na przykład w [1] i [2]. Warto przy okazji nadmienić, że Władimir Drinfeld - autor wspomnianej nierówności - był laureatem Medalu Fieldsa w 1990 roku, a niedawno (w 2018 roku) otrzymał Nagrodę Wolfa w dziedzinie matematyki.
Okazuje się, że dla 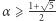 zachodzi nierówność
zachodzi nierówność 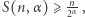 zaś równość ma miejsce wtedy i tylko wtedy, gdy wszystkie liczby w ciągu są równe. Dowód można odnaleźć w [5]. Zatem dla
zaś równość ma miejsce wtedy i tylko wtedy, gdy wszystkie liczby w ciągu są równe. Dowód można odnaleźć w [5]. Zatem dla 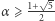 też wszystko jest jasne.
też wszystko jest jasne.
Pozostają więc do zbadania przypadki: 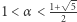 oraz
oraz 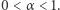 Dalej interesować nas będzie tylko ta druga sytuacja. Ustalmy liczby rzeczywiste
Dalej interesować nas będzie tylko ta druga sytuacja. Ustalmy liczby rzeczywiste 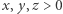 oraz
oraz 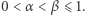 Niech
Niech 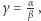 wówczas
wówczas 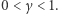 Mamy
Mamy
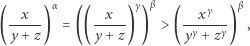 |
bo jeżeli 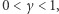 to
to
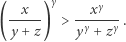 |
Wobec tego dla wszystkich wykładników 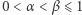 zachodzi nierówność
zachodzi nierówność 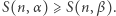
Z rozwiązania problemu Shapiro i powyższej uwagi wnioskujemy, że dla parzystych liczb 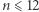 i wszystkich wykładników
i wszystkich wykładników 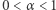 zachodzi
zachodzi 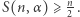 Liczby
Liczby 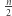 nie można tu zastąpić liczbą większą, wystarczy bowiem rozważyć 1, 0, 1, 0, …, 1, 0. Zatem dla parzystych liczb
nie można tu zastąpić liczbą większą, wystarczy bowiem rozważyć 1, 0, 1, 0, …, 1, 0. Zatem dla parzystych liczb 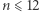 i wszystkich wykładników
i wszystkich wykładników 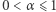 mamy pełną odpowiedź:
mamy pełną odpowiedź: 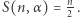
Rozumując podobnie jak w firmowym rozwiązaniu zadania 766 (zobacz Delta 1/2019), możemy udowodnić nierówność 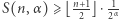 dla wszystkich
dla wszystkich 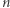 i
i 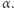 Z drugiej strony, rozważając ciąg
Z drugiej strony, rozważając ciąg 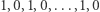 dla
dla 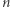 parzystych lub
parzystych lub 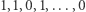 (dwie jedynki sąsiadują) dla
(dwie jedynki sąsiadują) dla 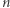 nieparzystych, dostajemy
nieparzystych, dostajemy 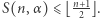 Ponieważ
Ponieważ 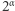 zbiega do 1, gdy
zbiega do 1, gdy 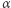 dąży do 0, więc naturalna jest hipoteza, że dla bliskich 0 wartości wykładnika
dąży do 0, więc naturalna jest hipoteza, że dla bliskich 0 wartości wykładnika 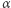 zachodzi
zachodzi 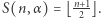 Jak zauważyliśmy wyżej, jest ona spełniona dla parzystych
Jak zauważyliśmy wyżej, jest ona spełniona dla parzystych 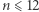 i wszystkich wykładników
i wszystkich wykładników 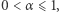 gdyż dla parzystych
gdyż dla parzystych 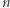 mamy
mamy 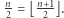
Dla 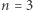 oraz
oraz 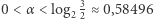 i dla dowolnych dodatnich liczb
i dla dowolnych dodatnich liczb 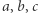 prawdziwa jest nierówność
prawdziwa jest nierówność
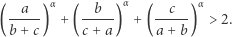 |
Jest to udowodnione w [3]. Zatem 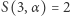 dla
dla 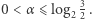 Oczywiście dla
Oczywiście dla 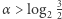 jest
jest 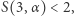 co widać na przykładzie liczb
co widać na przykładzie liczb 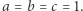 Dla
Dla 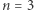 oraz dla parzystych liczb
oraz dla parzystych liczb 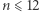 wszystko jest więc jasne.
wszystko jest więc jasne.
Na podstawie udowodnionej wyżej nierówności 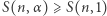 dla
dla 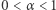 oraz tego, co wiadomo z rozwiązania problemu Shapiro, otrzymujemy, że
oraz tego, co wiadomo z rozwiązania problemu Shapiro, otrzymujemy, że 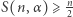 dla liczb nieparzystych
dla liczb nieparzystych 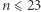 oraz
oraz 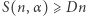 dla pozostałych wartości
dla pozostałych wartości 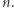
Kierując się wyłącznie intuicją, postawiłem hipotezę, że 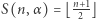 dla wszystkich
dla wszystkich 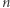 oraz
oraz 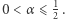 Nie potrafię tego dowieść dla żadnej liczby
Nie potrafię tego dowieść dla żadnej liczby 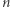 poza wskazanymi powyżej (czyli dla
poza wskazanymi powyżej (czyli dla 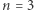 oraz parzystych
oraz parzystych 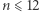 ). O sytuacji dla pozostałych wartości
). O sytuacji dla pozostałych wartości 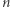 mogę powiedzieć bardzo niewiele. Jedynie dla
mogę powiedzieć bardzo niewiele. Jedynie dla 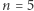 (najmniejsza niezbadana wartość
(najmniejsza niezbadana wartość 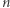 ) udało mi się pokazać, że
) udało mi się pokazać, że 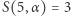 dla
dla 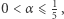 co stanowi pełne rozwiązanie zadania 766. Dowód udostępniony jest na stronie Delty. Będę bardzo wdzięczny za wszelkie uwagi lub związane wyniki. Na przykład dowody nierówności postaci
co stanowi pełne rozwiązanie zadania 766. Dowód udostępniony jest na stronie Delty. Będę bardzo wdzięczny za wszelkie uwagi lub związane wyniki. Na przykład dowody nierówności postaci 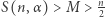 dla nieparzystych
dla nieparzystych 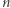 i możliwie dużych
i możliwie dużych 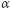 (najlepiej
(najlepiej 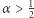 ) lub ewentualne kontrprzykłady do uczynionych wyżej hipotez. Zapraszam do kontaktu poprzez adres poczty elektronicznej, a także do dyskusji w komentarzach do tego artykułu na stronie Delty. Według mojej wiedzy w literaturze ani w sieci nie ma aktualnie żadnych innych tego rodzaju wyników. Uzyskanie takowych może więc być cenne, w szczególności dla osób zainteresowanych Konkursem Prac Uczniowskich z Matematyki im. Pawła Domańskiego.
) lub ewentualne kontrprzykłady do uczynionych wyżej hipotez. Zapraszam do kontaktu poprzez adres poczty elektronicznej, a także do dyskusji w komentarzach do tego artykułu na stronie Delty. Według mojej wiedzy w literaturze ani w sieci nie ma aktualnie żadnych innych tego rodzaju wyników. Uzyskanie takowych może więc być cenne, w szczególności dla osób zainteresowanych Konkursem Prac Uczniowskich z Matematyki im. Pawła Domańskiego.
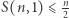 ; wystarczy rozpatrzeć ciąg samych jedynek.
; wystarczy rozpatrzeć ciąg samych jedynek.