Średnie w zawodach studenckich
Czytelnicy Delty zapewne znają zawody matematyczne dla uczniów, takie jak Olimpiada Matematyczna lub Kangur Matematyczny. Nie wszyscy wiedzą jednak, że konkursowe zmagania można kontynuować również podczas studiów. Na niektórych uczelniach odbywają się nawet specjalne zajęcia, podczas których rozwiązuje się i omawia zadania konkursowe.
Przyjrzyjmy się bliżej często używanemu podczas zawodów studenckich twierdzeniu o wartości średniej, przypisywanemu Lagrange'owi.
Twierdzenie (o wartości średniej). Dla funkcji ciągłej ![| f [a,b] R](/math/temat/matematyka/analiza/2019/11/29/Srednie_w_zawodach_studenckich/1x-88876efe12326637e9c77c7845d3af9c5b67a139-im-33,33,33-FF,FF,FF.gif) i różniczkowalnej w przedziale
i różniczkowalnej w przedziale 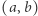 istnieje punkt
istnieje punkt  w przedziale
w przedziale 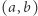 taki, że
taki, że

Inaczej mówiąc, przyrost wartości funkcji wyraża się przez przyrost wartości zmiennej i pochodną funkcji w pewnym punkcie pośrednim.
Równie przydatne jest uogólnienie powyższego twierdzenia, znane jako twierdzenie Cauchy'ego. Mianowicie, dla funkcji ciągłych ![| f,g [a,b] R](/math/temat/matematyka/analiza/2019/11/29/Srednie_w_zawodach_studenckich/1x-961d7c85c4a46b97a145acab167ea9759613b04a-im-33,33,33-FF,FF,FF.gif) i różniczkowalnych w przedziale
i różniczkowalnych w przedziale 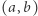 istnieje punkt
istnieje punkt  w przedziale
w przedziale 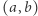 taki, że
taki, że

Zauważmy, że biorąc w twierdzeniu Cauchy'ego funkcję 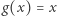 dla każdego
dla każdego 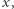 uzyskujemy twierdzenie Lagrange'a.
uzyskujemy twierdzenie Lagrange'a.
Jesteśmy gotowi, aby zastosować powyższe twierdzenia do rozwiązywania zadań z międzynarodowych zawodów dla studentów. Rozważmy różniczkowalną funkcję ![f [0,1] [0,1]](/math/temat/matematyka/analiza/2019/11/29/Srednie_w_zawodach_studenckich/1x-5912cf0e4391afc0182e7adcfc6d6a27438ca387-im-33,33,33-FF,FF,FF.gif) taką, że
taką, że 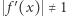 dla wszystkich
dla wszystkich 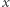 z przedziału
z przedziału ![[0,1].](/math/temat/matematyka/analiza/2019/11/29/Srednie_w_zawodach_studenckich/4x-5912cf0e4391afc0182e7adcfc6d6a27438ca387-im-33,33,33-FF,FF,FF.gif) Udowodnimy, że równości
Udowodnimy, że równości 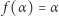 i
i 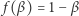 są spełnione dla co najwyżej jednej pary liczb
są spełnione dla co najwyżej jednej pary liczb 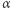 i
i 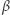 z przedziału
z przedziału ![[0,1].](/math/temat/matematyka/analiza/2019/11/29/Srednie_w_zawodach_studenckich/9x-5912cf0e4391afc0182e7adcfc6d6a27438ca387-im-33,33,33-FF,FF,FF.gif) Założywszy, że
Założywszy, że 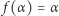 i
i 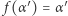 dla
dla 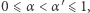 z twierdzenia Lagrange'a otrzymujemy, że istnieje
z twierdzenia Lagrange'a otrzymujemy, że istnieje 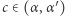 takie, że
takie, że

więc 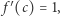 ale to jest sprzeczne z założeniem
ale to jest sprzeczne z założeniem 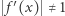 dla
dla ![|x∈ [0,1].](/math/temat/matematyka/analiza/2019/11/29/Srednie_w_zawodach_studenckich/17x-5912cf0e4391afc0182e7adcfc6d6a27438ca387-im-33,33,33-FF,FF,FF.gif) Podobnie wykluczamy istnienie dwóch elementów
Podobnie wykluczamy istnienie dwóch elementów 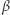 o własności
o własności 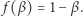 Dowód pozostawiamy Czytelnikowi jako ćwiczenie, Ambitnemu Czytelnikowi proponujemy pokazanie istnienia pary punktów
Dowód pozostawiamy Czytelnikowi jako ćwiczenie, Ambitnemu Czytelnikowi proponujemy pokazanie istnienia pary punktów 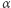 i
i 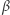 o powyższych własnościach. W ten sposób zostanie uzyskane rozwiązanie zadania 1. w kategorii I z 22. Zawodów im. Vojtěcha Jarníka.
o powyższych własnościach. W ten sposób zostanie uzyskane rozwiązanie zadania 1. w kategorii I z 22. Zawodów im. Vojtěcha Jarníka.
Okazuje się, że twierdzenie o wartości średniej może zostać zastosowane także do rozwiązywania równań. Rozważmy następujące równanie:

Rozwiązanie tego równania zostało postawione jako problem 1. w kategorii II podczas 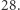 Zawodów V. Jarníka.
Zawodów V. Jarníka.
Rozwiązanie rozpoczniemy od prostej obserwacji, że liczba 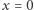 jest rozwiązaniem powyższego równania. Przyjmijmy zatem, że
jest rozwiązaniem powyższego równania. Przyjmijmy zatem, że 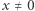 również jest rozwiązaniem. Równanie możemy przepisać w następujący sposób:
również jest rozwiązaniem. Równanie możemy przepisać w następujący sposób:
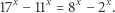 |
(*) |
Niech 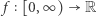 będzie funkcją określoną wzorem
będzie funkcją określoną wzorem 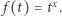 Funkcja ta spełnia założenia twierdzenia Lagrange'a na odcinku
Funkcja ta spełnia założenia twierdzenia Lagrange'a na odcinku ![|[2,8].](/math/temat/matematyka/analiza/2019/11/29/Srednie_w_zawodach_studenckich/6x-ff323b8f62bbf2624b1f6868f512023782429792-im-33,33,33-FF,FF,FF.gif) Zatem istnieje taka liczba
Zatem istnieje taka liczba 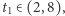 że
że

Funkcja ta spełnia również założenia tegoż twierdzenia na odcinku ![|[11,17],](/math/temat/matematyka/analiza/2019/11/29/Srednie_w_zawodach_studenckich/9x-ff323b8f62bbf2624b1f6868f512023782429792-im-33,33,33-FF,FF,FF.gif) więc istnieje liczba
więc istnieje liczba 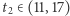 spełniająca zależność
spełniająca zależność

Zauważmy, że 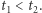 Podstawiając otrzymane zależności (przypomnijmy, że
Podstawiając otrzymane zależności (przypomnijmy, że  jest rozwiązaniem) do równania (*), dostajemy równość
jest rozwiązaniem) do równania (*), dostajemy równość

którą możemy przepisać równoważnie jako

Ponieważ 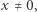 to
to 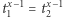 i w konsekwencji
i w konsekwencji

Skoro 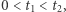 to
to 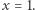 Łatwo sprawdzić, że
Łatwo sprawdzić, że 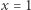 jest również rozwiązaniem równania. Zatem jedynymi rozwiązaniami są
jest również rozwiązaniem równania. Zatem jedynymi rozwiązaniami są 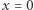 oraz
oraz 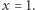
Twierdzenie o wartości średniej może także przynieść zaskakująco proste rozwiązanie zadania, które początkowo zdaje się wymagać zupełnie innych metod. Wykażemy, że jeśli

to wielomian 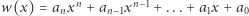 ma dodatni pierwiastek rzeczywisty. To zadanie nie pochodzi wprawdzie bezpośrednio z zawodów matematycznych, ale jest motywowane zadaniem 2.10.1. z bardzo dobrego zbioru zadań: T. Andreescu, R. Gelca, Mathematical Olympiad Challenges.
ma dodatni pierwiastek rzeczywisty. To zadanie nie pochodzi wprawdzie bezpośrednio z zawodów matematycznych, ale jest motywowane zadaniem 2.10.1. z bardzo dobrego zbioru zadań: T. Andreescu, R. Gelca, Mathematical Olympiad Challenges.
Kiedy już wiemy, że chcemy wykorzystać twierdzenie o wartości średniej, to nie pozostaje nic innego, jak znaleźć odpowiednią funkcję. Chcemy udowodnić istnienie punktu, w którym zeruje się dany wielomian, dlatego pierwszym słusznym pomysłem jest rozważenie funkcji

której pochodną jest właśnie 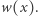 Pozostaje zauważyć, że
Pozostaje zauważyć, że

Zatem na mocy twierdzenia Rolle'a, które jest szczególnym przypadkiem twierdzenia Lagrange'a dla 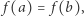 wnioskujemy istnienie punktu
wnioskujemy istnienie punktu 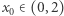 takiego, że
takiego, że 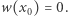
Mamy nadzieję, że przekonaliśmy Czytelnika do tego, że twierdzenia o wartości średniej mogą być bardzo użyteczne podczas rozwiązywania zadań w trakcie międzynarodowych zawodów matematycznych - i nie tylko...