Co to jest?
Drobiazgi
Ciągłość
Ciągłość funkcji - na początku odwołamy się do intuicyjnego rozumienia tego pojęcia, by następnie je uściślić...

Rys. 1. Wykres funkcji 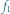
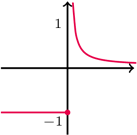
Rys. 2. Wykres funkcji 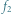
Jeśli funkcja rzeczywista określona na przedziale jest ciągła, to jej wykres jest "w jednym kawałku" (można go narysować bez odrywania ołówka od kartki). Funkcje
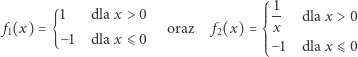
nie są ciągłe - w obu przypadkach 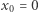 jest argumentem, w którym wykres funkcji "rozrywa się"; jest to tzw. punkt nieciągłości funkcji. Funkcja ciągła nie może mieć punktów nieciągłości, czyli w każdym punkcie swojej dziedziny musi być ciągła. Pozostaje ściśle określić, co to wszystko znaczy. Ciągłość funkcji w punkcie można wyrazić w języku zbieżności ciągów:
jest argumentem, w którym wykres funkcji "rozrywa się"; jest to tzw. punkt nieciągłości funkcji. Funkcja ciągła nie może mieć punktów nieciągłości, czyli w każdym punkcie swojej dziedziny musi być ciągła. Pozostaje ściśle określić, co to wszystko znaczy. Ciągłość funkcji w punkcie można wyrazić w języku zbieżności ciągów:
Definicja. Funkcja 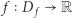 jest ciągła w
jest ciągła w 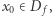 jeśli dla każdego ciągu o wyrazach
jeśli dla każdego ciągu o wyrazach 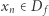 zbieżnego do
zbieżnego do 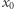 ciąg
ciąg 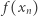 jest zbieżny do
jest zbieżny do 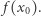
Łatwo teraz sprawdzić formalnie, przyjmując 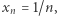 że funkcje
że funkcje 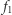 i
i 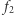 nie są ciągłe w zerze - ciągi o wyrazach
nie są ciągłe w zerze - ciągi o wyrazach 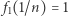 (ciąg stały) oraz
(ciąg stały) oraz 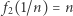 nie są zbieżne do
nie są zbieżne do 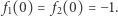
Gdy już wiemy, czym są funkcje ciągłe, zauważmy, że jest ich mnóstwo w otaczającym nas świecie - przyjrzyjmy się tylko funkcjom zależnym od czasu: temperatura w nagrzewającym się piekarniku zmienia się w sposób ciągły, ciśnienie w punkcie pomiarowym również, prędkość samochodu, nawet takiego z super mocnym silnikiem i hamulcami, nie może zmieniać się skokowo.
Warto podkreślić, że o ciągłości funkcji można mówić tylko w punktach jej dziedziny. Gdybyśmy przyjęli, że dziedziną funkcji 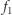 i
i 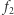 jest
jest 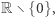 to byłyby one ciągłe w każdym punkcie swojej dziedziny, a więc byłyby funkcjami ciągłymi (mimo, że ich wykresy składają się z dwóch "kawałków"). Podobnie funkcja tangens jest ciągła, mimo iż jej wykres ma nieskończenie wiele składowych.
to byłyby one ciągłe w każdym punkcie swojej dziedziny, a więc byłyby funkcjami ciągłymi (mimo, że ich wykresy składają się z dwóch "kawałków"). Podobnie funkcja tangens jest ciągła, mimo iż jej wykres ma nieskończenie wiele składowych.
Istnieją funkcje, które nie są ciągłe w żadnym punkcie swojej dziedziny; sztandarowym przykładem jest funkcja Dirichleta, która przyjmuje wartość 0 dla wszystkich argumentów wymiernych i 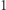 dla wszystkich niewymiernych.
dla wszystkich niewymiernych.
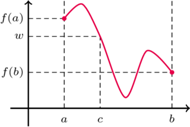
Rys. 3. Ilustracja własności Darboux
Funkcje ciągłe są bohaterami wielu ważnych twierdzeń matematycznych. Jedno z nich orzeka, że funkcja ciągła określona na przedziale posiada własność Darboux, czyli przyjmuje wszystkie wartości pośrednie: dla dowolnych 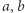 w tym przedziale oraz
w tym przedziale oraz 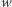 leżącego między
leżącego między 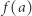 i
i 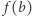 istnieje
istnieje ![|c∈ [a,b],](/math/temat/matematyka/analiza/2019/03/25/Ciaglosc/5x-ecb45ea0d1cd47e433433fa4bcf1b25b15e746a2-im-33,33,33-FF,FF,FF.gif) dla którego
dla którego 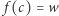 (Rys. 3). Funkcje o własności Darboux nie muszą być jednak ciągłe. Istnieją takie ekstremalne przykłady funkcji, dla których obraz dowolnego przedziału jest całą prostą rzeczywistą! Taka funkcja oczywiście spełnia własność Darboux i oczywiście nie może być ciągła (dlaczego?). Czytelniku, czy potrafisz skonstruować takiego potwora?
(Rys. 3). Funkcje o własności Darboux nie muszą być jednak ciągłe. Istnieją takie ekstremalne przykłady funkcji, dla których obraz dowolnego przedziału jest całą prostą rzeczywistą! Taka funkcja oczywiście spełnia własność Darboux i oczywiście nie może być ciągła (dlaczego?). Czytelniku, czy potrafisz skonstruować takiego potwora?
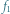
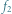
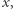 dla którego spełniona jest równość
dla którego spełniona jest równość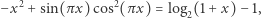
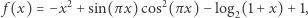
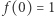 i
i 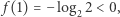 zatem dla pewnego
zatem dla pewnego 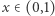 funkcja przyjmuje wartość zero i ten właśnie
funkcja przyjmuje wartość zero i ten właśnie 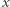 jest rozwiązaniem naszego równania.
jest rozwiązaniem naszego równania.