Co to jest?
Drobiazgi
Zbieżność
Zbieżność to jedno z najważniejszych pojęć analizy matematycznej, odnoszące się najczęściej do ciągów i funkcji (oraz rozmaitych obiektów matematycznych skonstruowanych przy ich użyciu, np. szeregów czy ciągów funkcyjnych). Tu zajmiemy się zbieżnością ciągów liczbowych.

Rys. 1. Gdyby 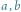 były granicami pewnego ciągu, to w każdym z kolorowych przedziałów musiałyby znaleźć się prawie wszystkie wyrazy tego ciągu, a to jest sprzeczność.
były granicami pewnego ciągu, to w każdym z kolorowych przedziałów musiałyby znaleźć się prawie wszystkie wyrazy tego ciągu, a to jest sprzeczność.
Mówimy, że ciąg liczbowy 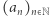 jest zbieżny, jeśli istnieje taka liczba
jest zbieżny, jeśli istnieje taka liczba 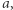 że dowolnie blisko niej znajdują się prawie wszystkie (czyli wszystkie poza skończoną liczbą) wyrazy ciągu. Innymi słowy, jeśli dla każdego
że dowolnie blisko niej znajdują się prawie wszystkie (czyli wszystkie poza skończoną liczbą) wyrazy ciągu. Innymi słowy, jeśli dla każdego 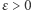 możemy odrzucić skończoną liczbę początkowych wyrazów ciągu, tak by wszystkie pozostałe należały do przedziału
możemy odrzucić skończoną liczbę początkowych wyrazów ciągu, tak by wszystkie pozostałe należały do przedziału 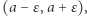 to mówimy, że ciąg jest zbieżny do
to mówimy, że ciąg jest zbieżny do  , i oznaczamy
, i oznaczamy 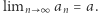 Z tej definicji w łatwy sposób wynika na przykład, że ciąg może mieć co najwyżej jedną granicę (Rys. 1).
Z tej definicji w łatwy sposób wynika na przykład, że ciąg może mieć co najwyżej jedną granicę (Rys. 1).
Przykładem ciągu zbieżnego jest ciąg 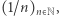 który jest zbieżny do zera. Ciągi, które nie są zbieżne, nazywamy rozbieżnymi. Rozbieżny jest np. ciąg o wyrazach
który jest zbieżny do zera. Ciągi, które nie są zbieżne, nazywamy rozbieżnymi. Rozbieżny jest np. ciąg o wyrazach 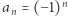 ; istotnie, nie może on spełniać definicji zbieżności - żaden przedział długości 1 (co odpowiada
; istotnie, nie może on spełniać definicji zbieżności - żaden przedział długości 1 (co odpowiada 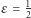 ) nie zawiera prawie wszystkich wyrazów tego ciągu.
) nie zawiera prawie wszystkich wyrazów tego ciągu.
Warto wspomnieć o szczególnym przypadku ciągów, które nie są zbieżne - o ciągach rozbieżnych do nieskończoności (nazywanych również ciągami zbieżnymi do granicy niewłaściwej). Są to ciągi spełniające następujący warunek: dla dowolnej liczby 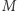 można odrzucić skończenie wiele wyrazów ciągu, tak by wszystkie pozostałe były większe od
można odrzucić skończenie wiele wyrazów ciągu, tak by wszystkie pozostałe były większe od 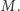 Rozbieżny do nieskończoności jest oczywiście ciąg
Rozbieżny do nieskończoności jest oczywiście ciąg 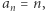 a także ciąg o wyrazach
a także ciąg o wyrazach 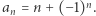
Pojęcie zbieżności pozwala zdefiniować sumę nieskończenie wielu liczb, czyli szereg. Dodawanie jest działaniem dwuargumentowym, w jednym kroku umiemy dodać tylko dwie liczby, więc aby dodać nieskończenie wiele liczb, trzeba by wykonać nieskończenie wiele kroków, a tego zrobić nie umiemy. I tu z pomocą przychodzi nam granica ciągu. Sumę nieskończenie wielu wyrazów 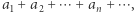 zapisywaną skrótowo jako
zapisywaną skrótowo jako 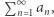 definiujemy jako granicę sumy ciągu
definiujemy jako granicę sumy ciągu 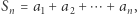 zwanego ciągiem sum częściowych. Możemy zatem wyznaczyć sumę wyrazów ciągu geometrycznego o wyrazach
zwanego ciągiem sum częściowych. Możemy zatem wyznaczyć sumę wyrazów ciągu geometrycznego o wyrazach 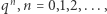 dla
dla 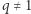 suma częściowa ma postać
suma częściowa ma postać 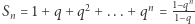 (wzór ten łatwo udowodnić, mnożąc obie strony równości przez
(wzór ten łatwo udowodnić, mnożąc obie strony równości przez 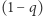 ). Dla
). Dla 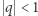 granica ciągu
granica ciągu 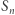 jest równa
jest równa 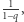 dla
dla 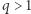 jest nieskończona, a dla
jest nieskończona, a dla 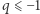 nie umiemy określić szukanej sumy (bo ciąg
nie umiemy określić szukanej sumy (bo ciąg 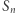 nie ma granicy).
nie ma granicy).
Warto dodać na koniec, że sumując wyrazy ciągu zbieżnego do zera, możemy uzyskać sumę nieskończoną - sztandarowym przykładem jest szereg harmoniczny, czyli suma
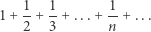
Rozbieżność do nieskończoności sumy 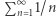 nie jest oczywista, ale dowód tego faktu nie jest szczególnie trudny. (Można go znaleźć w Delcie 07/2016).
nie jest oczywista, ale dowód tego faktu nie jest szczególnie trudny. (Można go znaleźć w Delcie 07/2016).
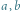 były granicami pewnego ciągu, to w każdym z kolorowych przedziałów musiałyby znaleźć się prawie wszystkie wyrazy tego ciągu, a to jest sprzeczność.
były granicami pewnego ciągu, to w każdym z kolorowych przedziałów musiałyby znaleźć się prawie wszystkie wyrazy tego ciągu, a to jest sprzeczność.