Niewąskie nierówności

Nierówności między średnimi, a w szczególności nierówność między średnią arytmetyczną i geometryczną (oznaczana dalej A-G), to jedne z podstawowych narzędzi dowodowych w arsenale każdego olimpijczyka...

Przypomnijmy sformułowanie A-G:

Twierdzenie. Dla dowolnego ciągu $n$ nieujemnych liczb 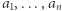$|a1,...,an$ spełniona jest nierówność

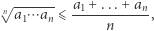
n√ a-⋯-a-⩽ a1-+...+-an-, 1 n n

przy czym równość zachodzi wtedy i tylko wtedy, gdy 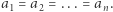$|a1 = a2 = ... = an.$

Twierdzenie to dowodzone jest zwykle indukcyjnie lub za pomocą twierdzenia Jensena, ale jeśli dowody te pozostawiły w Tobie, drogi Czytelniku, niedosyt i wciąż masz wrażenie, że nierówność A-G pozostaje nieintuicyjna, być może znajdziesz ukojenie w poniższym rozumowaniu. Naturalnie, tych, którzy nie widzieli jeszcze żadnego dowodu A-G, również zapraszamy do lektury.

Na początek przedstawimy dwie obserwacje, które powinny się wydać oczywiste każdemu zaznajomionemu z pojęciem średniej arytmetycznej:

Biorąc dowolne dwie spośród liczb 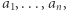$a1,...,an,$ a następnie zwiększając jedną z nich o 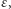$ε,$ a drugą zmniejszając o $ε$ (gdzie $ε$ jest dowolną liczbą dodatnią), nie zmienimy wartości średniej arytmetycznej liczb $a1,...,an.$
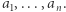
Jeśli jedna z liczb 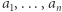$|a,...,a 1 n$ jest większa od średniej arytmetycznej tych liczb, to jest też pośród nich liczba mniejsza od tej średniej i vice versa.

Proste? No więc możemy iść dalej.

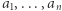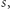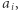
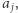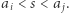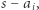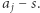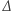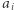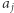Następnym krokiem będzie zdefiniowanie operacji zwężania do średniej. Mając dany ciąg liczb $a1,...,an$ o średniej arytmetycznej $s,$ weźmy takie dowolne dwie $|ai,$ $a j,$ że $|ai < s < a j.$ Mniejsza jest odległa od średniej o $|s− a , i$ a większa o $|a − s. j$ Niech $|∆$ będzie mniejszą z tych dwóch różnic. Zwężenie do średniej liczb $|ai$ i $|a j$ polega na jednoczesnym zmniejszeniu 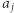$a j$ i zwiększeniu 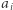$|ai$ o 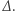$∆ .$ Przykładowo, jeśli w zadanym ciągu liczb średnia arytmetyczna wynosiła 7, to liczby 13 i 2 zostaną zwężone do liczb 8 i 7, a liczby 5 i 9 zwężone do 7 i 7.

Operacja zwężania ma trzy cechy godne odnotowania:

1.: Zwężenie dowolnych dwóch liczb z ciągu nie zmienia średniej arytmetycznej całego ciągu.
2.: Za każdym razem gdy dokonujemy zwężenia, przynajmniej jedna ze zwężanych liczb zrównuje się ze średnią.
3.: Za pomocą skończonej liczby operacji zwężania możemy zrównać wszystkie zadane liczby z ich średnią.

Jeśli w tym momencie, Szanowny Czytelniku, zmarszczyłeś brwi poruszony myślą "Czy aby na pewno? Dla dowolnych ciągów 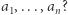$|a ,...,a ? 1 n$ W skończonej liczbie kroków?", spieszymy z wyjaśnieniami. Otóż, dopóki nie zrównamy wszystkich liczb ze średnią, zawsze będzie para liczb do zwężenia różnych od średniej. Zanim więc nie osiągniemy celu, możemy zwężać, a z każdym zwężeniem liczba liczb różnych od średniej zmniejsza się o jedną lub o dwie. Dla zilustrowania tego procesu przedstawiamy poniżej ciąg takich zwężeń dla liczb 8, 18, 6, 10, 21, 16, 26 (których średnia arytmetyczna wynosi 15), gdzie pogrubione zostały pary liczb podlegających zwężeniu.

$8, 18, 6, 10, 21, 16, 26 11, 15, 6, 10, 21, 16, 26 15, 15, 6, 10, 17, 16, 26 15, 15, 8, 10, 15, 16, 26 15, 15, 9, 10, 15, 15, 26 15, 15, 15, 10, 15, 15, 20 15, 15, 15, 15, 15, 15, 15$

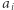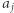Nadszedł czas na grande finale, w którym wyjaśni się, jaki był cel całego zamieszania ze zwężeniami. Jest jasne, że zwężanie nie zmienia wartości sumy liczb, a tym samym ich średniej arytmetycznej. Co natomiast z iloczynem, a w konsekwencji - ze średnią geometryczną? Zachowując poprzednio wprowadzone oznaczenia, załóżmy, bez utraty ogólności, że liczby $ai$ oraz $a j$ zwężamy o 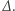$|∆.$ Iloczyn zmieni się wtedy na

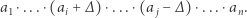
a1 ⋅...⋅(ai +∆ )⋅...⋅(a j −∆ )⋅...⋅an.

Wartość tego iloczynu będzie większa niż oryginalnego 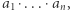$a1 ⋅...⋅an,$ gdyż

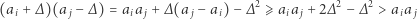
(a + ∆ )(a − ∆) = aa + ∆(a − a ) −∆ 2⩾ a a + 2∆ 2− ∆2 > a a i j ij j i i j i j

(w przedostatnim kroku skorzystaliśmy z nierówności 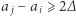$|a j− ai⩾ 2∆$ ). Widać więc, że zwężanie zwiększa iloczyn zwężanych liczb. Oznacza to, że średnia geometryczna wszystkich liczb również się zwiększa! Prawdziwość A-G powinna się teraz objawić w całej swojej oczywistości. Mając ciąg liczb, które nie są parami równe, dokonujemy skończonej liczby zwężeń aż do zrównania ich ze średnią arytmetyczną. Kiedy to nastąpi i wszystkie liczby z naszego ciągu będą parami równe, obie średnie także się zrównają. Ponieważ jednak z każdym zwężeniem średnia geometryczna zwiększała się, a arytmetyczna nie ulegała zmianom, wnioskujemy, iż dla wyjściowego ciągu średnia geometryczna była mniejsza od arytmetycznej. To kończy dowód.

Dociekliwym Czytelnikom pozostawiamy sprawdzenie, że analogicznie można przeprowadzić dowód nierówności:

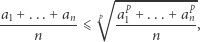
√ --p--------p a1 +-...+-an p a-1 +-...+-an n ⩽ n ,

gdzie 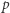$p$ jest dodatnią liczbą naturalną, a 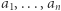$a1,...,an$ są nieujemnymi liczbami rzeczywistymi. Podpowiemy, iż należy zbadać, jak zwężanie liczb wpływa na wartość 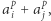$ap + ap, i j$ korzystając ze wzoru dwumianowego Newtona.

Nasuwa się pytanie, czy są inne nierówności między średnimi, które można udowodnić w analogiczny sposób, tzn. wynajdując przekształcenie ciągu danych liczb, podobne do powyższego zwężania do średniej? Takie przekształcenie powinno mieć dwie cechy:

nie zmieniając wartości jednej ze średnich, zawsze zwiększa (ew. zmniejsza) drugą z nich;
w skończonej liczbie kroków wyrównuje wszystkie liczby, tym samym wyrównując obie średnie.

Z tym pytaniem pozostawiamy Czytelnika.