Pierwiastki łańcuchowe

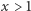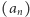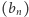Niech $|x > 1$ będzie ustaloną liczbą rzeczywistą. Rozważmy ciągi $|(an)$ i $(bn)$ określone rekurencyjnie wzorami

2 2 b1 = x, an = [bn − bn], bn+1 = bn − an dlan ∈N

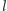(symbol $| [l]$ oznacza największą liczbę całkowitą nie większą od $| l$ ). Zauważmy najpierw, że wszystkie wyrazy ciągu 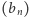$(bn)$ są dodatnie. Istotnie, mamy

bn+1 = b2 −an = b2 −[b2 − bn]⩾ b2 −(b2 − bn) = bn, n n n n n

a stąd wynika, że 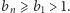$|bn ⩾b1 > 1.$ Skoro tak, to mamy także 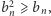$b2n ⩾bn,$ a więc 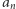$|a n$ są nieujemnymi liczbami całkowitymi.

Rozważmy teraz ciąg 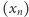$(xn)$ określony wzorem

√ ------------------- √ --------√---- xn = a1 + a2 + ⋯ + an dlan∈ N.

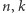Dla $n, k$ naturalnych, 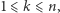$1⩽ k ⩽ n,$ oznaczmy 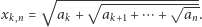$√ ----√---------------- |xk,n = ak + ak+1 + ⋯ + √ an.$ Wykażemy, że dla każdego 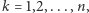$|k = 1,2,...,n,$ przy ustalonym 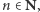$n ∈ N,$ zachodzi równość

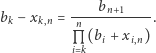----bn+1---- bk− xk,n = n . L (bi +xi,n) i k

(1)

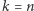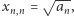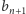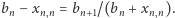
Dla $k = n$ istotnie tak jest, bowiem $√ --- √--- bn− an = (b2n− an)/(bn + an)$ i $√ --- xn,n = an,$ a zatem z definicji $|bn+1$ mamy $bn− xn,n = bn+1/(bn + xn,n).$

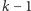Załóżmy prawdziwość równości (1) dla pewnego $k.$ Dla $k − 1$ mamy wówczas, na mocy założenia indukcyjnego,

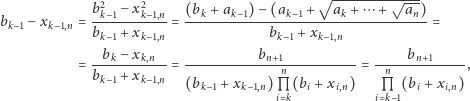
2 2 √ --------√---- b − x = b-k− 1-−xk−1,n = (bk +-ak−1)−-(ak−1 +-ak-+⋯-+--an)-= k−1 k−1,n bk−1 +xk−1,n bk−1 + xk−1,n = --bk-−xk,n- = ----------bn+1-----------= -----bn+1----, bk−1 +xk−1,n (b + x )Ln(b + x ) Ln (b + x ) k−1 k−1,n i k i i,n i k− 1 i i,n

co kończy dowód indukcyjny (proszę zauważyć, że była to indukcja do tyłu). W szczególności, dla 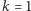$k = 1$ równość (1) przyjmuje postać

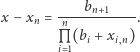bn+1 x −xn = -n----------. L (bi + xi,n) i 1

(2)

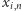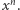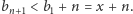Ponieważ $bi⩾ b1 = x,$ a liczby $|xi,n$ są nieujemne, więc mianownik ułamka po prawej stronie można oszacować z dołu przez $|xn.$ Z drugiej strony, $2 2 2 2 bn+1 = bn − [b n− bn] < bn − (bn− bn− 1) = bn + 1,$ a stąd przez indukcję dostajemy $bn+1 < b1 + n = x + n.$ Ostatecznie, z równości (2) otrzymujemy

x − x ⩽ x-+n-. n xn

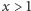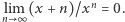Wobec nierówności $x > 1$ mamy $n lni m∞ (x +n)/x = 0.$ Zatem ciąg 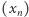$|(xn)$ jest zbieżny do 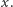$x.$ Udowodniliśmy w ten sposób

Twierdzenie. Dla każdej liczby rzeczywistej 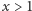$x > 1$ istnieje taki ciąg 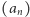$(an)$ liczb całkowitych nieujemnych, że ciąg $√ ----√--------------- |xn = a1 + a2 + ⋯ + √ an$ jest zbieżny do $x.$

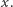
Przykład.

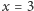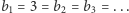Dla $|x = 3$ mamy $b1 = 3 = b2 = b3 = ...$ oraz $a1 = [32 −3] = 6 = a2 = a3 = ...$
Ogólnie, dla dowolnej liczby naturalnej $|n > 1,$ mamy $√ ------------------------------ 2 √ 2 √ -2-------- n = n − n + n − n + n − n +⋯ .$
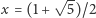Gdy $√ -- x = (1+ 5)/2$ jest współczynnikiem złotej proporcji, wszystkie wyrazy ciągu 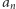$an$ są równe 1.