e z gumy
Jak znaleźć 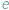 na gitarze? Nawet początkujący gitarzysta wie, że przy standardowym nastrojeniu właśnie taki dźwięk wydają dwie skrajne struny. My jednak będziemy szukać innego
na gitarze? Nawet początkujący gitarzysta wie, że przy standardowym nastrojeniu właśnie taki dźwięk wydają dwie skrajne struny. My jednak będziemy szukać innego 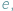 a mianowicie pewnej znanej i przydatnej stałej matematycznej. Powiedzmy, że z jakiegoś powodu chcemy poddać próbie wytrzymałość strun. W tym celu kręcimy kołkiem do momentu, w którym długość nawiniętej na niego części struny będzie taka sama, jak długość części nienawiniętej. Pytanie brzmi: ilukrotnie w takim procesie musiałaby rozciągnąć się struna? Aby udzielić na nie odpowiedzi, rozważymy analogiczną sytuację, w której zamiast strun przyglądamy się gumie.
a mianowicie pewnej znanej i przydatnej stałej matematycznej. Powiedzmy, że z jakiegoś powodu chcemy poddać próbie wytrzymałość strun. W tym celu kręcimy kołkiem do momentu, w którym długość nawiniętej na niego części struny będzie taka sama, jak długość części nienawiniętej. Pytanie brzmi: ilukrotnie w takim procesie musiałaby rozciągnąć się struna? Aby udzielić na nie odpowiedzi, rozważymy analogiczną sytuację, w której zamiast strun przyglądamy się gumie.
Rys. 1
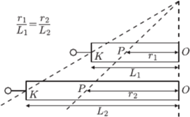
Uzbrójmy się zatem w długi pas rozciągliwej gumy, której jeden koniec unieruchamiamy w początkowym punkcie zaczepienia 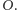 Drugi koniec wyposażamy w uchwyt, by dało się ją swobodnie rozciągać. Potrzebna też będzie powierzchnia (np. stół), na której kładziemy gumę tak, aby można było wygodnie mierzyć odległości. Zwróćmy uwagę, że rozciąganie gumy nie zmienia stosunku odległości między umieszczonymi na niej punktami. Ściślej, dla pewnego punktu
Drugi koniec wyposażamy w uchwyt, by dało się ją swobodnie rozciągać. Potrzebna też będzie powierzchnia (np. stół), na której kładziemy gumę tak, aby można było wygodnie mierzyć odległości. Zwróćmy uwagę, że rozciąganie gumy nie zmienia stosunku odległości między umieszczonymi na niej punktami. Ściślej, dla pewnego punktu 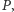 zaznaczonego na gumie, jeśli
zaznaczonego na gumie, jeśli 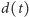 oznacza jego odległość od punktu zaczepienia
oznacza jego odległość od punktu zaczepienia 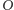 w chwili
w chwili 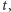 a
a 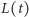 długość gumy, to zachodzi proporcja
długość gumy, to zachodzi proporcja
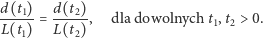 |
(1) |
Można więc wprowadzić wielkość 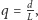 opisującą umiejscowienie punktu na gumie, niezależną od rozciągnięcia gumy. Różniczkując równanie
opisującą umiejscowienie punktu na gumie, niezależną od rozciągnięcia gumy. Różniczkując równanie 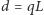 względem
względem 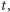 można otrzymać wyrażenie na prędkość
można otrzymać wyrażenie na prędkość 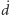 punktu
punktu 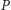
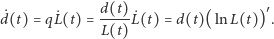 |
(2) |
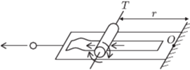
Rys. 2
W odległości  od
od 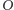 umieśćmy teraz nad gumą stykający się z nią, swobodnie obracający się walec, którego oś przytwierdzona jest do stołu. Rozciągająca się pod nim guma będzie powodowała jego obrót. Za pomocą wstęgi materiału umieszczonej między walcem a gumą możemy zmierzyć długość drogi, jaką przebył punkt dowolnie ustalony na obwodzie walca (Rys. 2) i wielkość tę oznaczymy przez
umieśćmy teraz nad gumą stykający się z nią, swobodnie obracający się walec, którego oś przytwierdzona jest do stołu. Rozciągająca się pod nim guma będzie powodowała jego obrót. Za pomocą wstęgi materiału umieszczonej między walcem a gumą możemy zmierzyć długość drogi, jaką przebył punkt dowolnie ustalony na obwodzie walca (Rys. 2) i wielkość tę oznaczymy przez 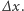 Przyjmijmy, że rozciąganie przebiega w przedziale czasowym
Przyjmijmy, że rozciąganie przebiega w przedziale czasowym 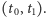 Okazuje się, że wygodnie będzie obliczyć szukaną wartość, zaczynając od wyznaczenia prędkości
Okazuje się, że wygodnie będzie obliczyć szukaną wartość, zaczynając od wyznaczenia prędkości 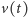 przesuwania się gumy pod walcem w dowolnej chwili
przesuwania się gumy pod walcem w dowolnej chwili 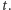 Z (2) można wywnioskować, że
Z (2) można wywnioskować, że
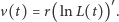 |
Aby wyznaczyć przesunięcie 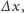 pozostaje scałkować funkcję
pozostaje scałkować funkcję 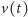 względem czasu w przedziale
względem czasu w przedziale 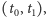 otrzymując
otrzymując 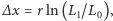 gdzie
gdzie 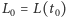 i
i 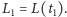 Zapiszmy uzyskany wynik w postaci
Zapiszmy uzyskany wynik w postaci
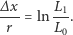 |
(3) |
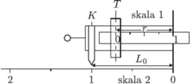
Rys. 3
Pasek materiału możemy teraz wyposażyć w skalę, na której za jednostkę przyjmujemy 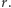 W ten sposób odczytana tam niemianowana wartość
W ten sposób odczytana tam niemianowana wartość 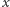 będzie wynosiła
będzie wynosiła 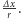 Umieśćmy też w punkcie końcowym
Umieśćmy też w punkcie końcowym 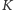 wskaźnik, którego przesunięcie będziemy mierzyć na drugiej skali, nieruchomej względem
wskaźnik, którego przesunięcie będziemy mierzyć na drugiej skali, nieruchomej względem 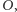 o jednostce
o jednostce 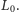 Jej wskazanie
Jej wskazanie 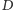 będzie więc wynosić
będzie więc wynosić 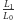 (Rys. 3). W ten sposób zależność (3) można uprościć do postaci
(Rys. 3). W ten sposób zależność (3) można uprościć do postaci
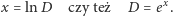 |
Powyższy związek między wskazaniami na skalach pozwala nam więc na doświadczalne wyznaczenie liczby  (poprzez rozciąganie do chwili, gdy wartość na skali pierwszej wyniesie 1 i odczytanie wyniku na skali drugiej) lub, na przykład,
(poprzez rozciąganie do chwili, gdy wartość na skali pierwszej wyniesie 1 i odczytanie wyniku na skali drugiej) lub, na przykład, 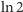 (poprzez dwukrotne rozciągnięcie gumy i odczytanie wyniku na skali pierwszej).
(poprzez dwukrotne rozciągnięcie gumy i odczytanie wyniku na skali pierwszej).
Rys. 4
Rys. 5
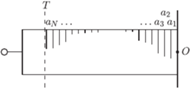
Zależność (3) można również wyznaczyć za pomocą mniej formalnego rozumowania, które nie wymaga całkowania funkcji. Połóżmy walec na końcu gumy, a między nim a początkiem gumy umieśćmy w równych odstępach 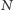 punktów pomiarowych i oznaczmy je, zaczynając od tego najbliżej
punktów pomiarowych i oznaczmy je, zaczynając od tego najbliżej 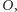 przez
przez 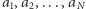 (Rys. 4). Niech
(Rys. 4). Niech 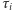 będzie momentem przejścia punktu
będzie momentem przejścia punktu 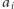 pod walcem. Obrót walca
pod walcem. Obrót walca 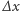 będziemy wyznaczać, sumując składowe obroty
będziemy wyznaczać, sumując składowe obroty 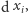 z których każdy mierzony jest od chwili
z których każdy mierzony jest od chwili 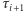 do chwili
do chwili 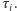 Przez
Przez 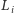 oznaczymy długość gumy w chwili
oznaczymy długość gumy w chwili 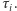 Zauważmy, że dla wystarczająco dużej liczby
Zauważmy, że dla wystarczająco dużej liczby 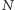 wartość
wartość 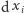 można przybliżyć przez
można przybliżyć przez 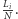 Oczywiste jest, że w chwili
Oczywiste jest, że w chwili 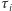 między walcem i początkiem gumy znajduje się
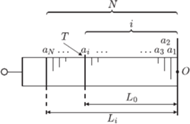
między walcem i początkiem gumy znajduje się 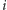 punktów pomiarowych, co z uwagi na równomierne rozmieszczenie punktów pomiarowych na gumie (Rys. 5) daje proporcję:
punktów pomiarowych, co z uwagi na równomierne rozmieszczenie punktów pomiarowych na gumie (Rys. 5) daje proporcję: 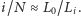 Jeśli końcowa długość gumy wyniosła
Jeśli końcowa długość gumy wyniosła 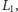 to z powyższej proporcji wynika, że rozciąganie zakończyło się w chwili
to z powyższej proporcji wynika, że rozciąganie zakończyło się w chwili 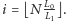 Wobec tego możemy obliczyć
Wobec tego możemy obliczyć
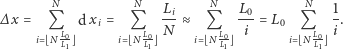 |
W tym miejscu możemy zastosować oszacowanie 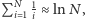 skąd wreszcie, pomijając znak części całkowitej:
skąd wreszcie, pomijając znak części całkowitej:
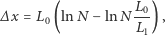 |
co jest równoważne z (3).
Rys. 6
Rys. 7
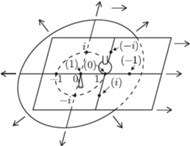
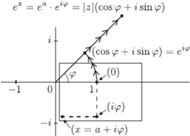
Powstaje naturalne pytanie, czy nasze urządzenie można ulepszyć w taki sposób, by demonstrowało działanie funkcji wykładniczej dla argumentów zespolonych. Teoretycznie jest to możliwe. Pas gumy zastępujemy kwadratową, gumową płachtą, unieruchomioną w jednym punkcie, względem którego może się ona obracać. Jej rozciąganie będzie się odbywać równomiernie w obu kierunkach, równoległych do krawędzi płachty. Także pas materiału używany do pomiaru należy zamienić na materiałową płachtę. Obie skale uzupełniamy o oś urojoną, a w miejscu walca umieszczamy kulę dociskającą materiał do gumy. Podczas ruchów gumy materiał ma się przesuwać, ale nie obracać. Załóżmy, że w wyniku pewnego obrotu i rozciągnięcia gumy znajdujący się na niej wskaźnik został przemieszczony do punktu 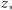 a wynik odczytany na skali materiałowej wyniósł
a wynik odczytany na skali materiałowej wyniósł 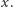 Wykorzystując wcześniejsze rozważania oraz fakt, że obrót gumy o kąt
Wykorzystując wcześniejsze rozważania oraz fakt, że obrót gumy o kąt 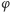 przekłada się na zmianę odczytu na skali materiałowej o
przekłada się na zmianę odczytu na skali materiałowej o 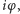 można stwierdzić, że wówczas
można stwierdzić, że wówczas 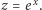 Nasza konstrukcja w naturalny sposób rozszerza więc definicję funkcji wykładniczej na zespolone argumenty. Niestety, jej wykonanie w warunkach domowych nie wydaje się możliwe i należy ją rozpatrywać raczej w kategoriach doświadczenia myślowego niż propozycji do samodzielnego wykonania.
Nasza konstrukcja w naturalny sposób rozszerza więc definicję funkcji wykładniczej na zespolone argumenty. Niestety, jej wykonanie w warunkach domowych nie wydaje się możliwe i należy ją rozpatrywać raczej w kategoriach doświadczenia myślowego niż propozycji do samodzielnego wykonania.
Mam nadzieję, że niniejszym tekstem choć na chwilę wyprowadziłem  z krainy matematycznych abstraktów i przekonałem Czytelnika, że nie trzeba wielkiego wysiłku, aby samemu je "upolować" w otaczającej nas rzeczywistości.
z krainy matematycznych abstraktów i przekonałem Czytelnika, że nie trzeba wielkiego wysiłku, aby samemu je "upolować" w otaczającej nas rzeczywistości.