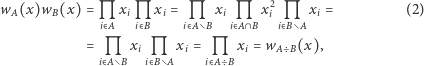Analiza na kostce dyskretnej
Kostką dyskretną wymiaru 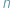 nazywamy
nazywamy 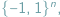 czyli zbiór wierzchołków kostki
czyli zbiór wierzchołków kostki ![[−1;1]n;](/math/temat/matematyka/analiza/2016/03/22/Analiza_na_kostce_dyskretnej/3x-ae19f29ba4da8a4c3f90055952d78d7be0629921-im-65,9A,A1-FF,FF,FF.gif) stanowiącej
stanowiącej 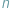 -wymiarowy odpowiednik sześcianu...
-wymiarowy odpowiednik sześcianu...
Rozważmy na niej działanie mnożenia po współrzędnych,

Nietrudno sprawdzić, że dla dowolnych wierzchołków kostki 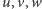 :
:
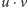 również jest wierzchołkiem kostki oraz
również jest wierzchołkiem kostki oraz 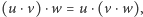
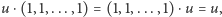 czyli
czyli 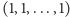 jest "wierzchołkiem neutralnym" przedstawionego działania,
jest "wierzchołkiem neutralnym" przedstawionego działania,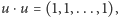 zatem dla każdego wierzchołka istnieje "wierzchołek odwrotny", czyli... on sam,
zatem dla każdego wierzchołka istnieje "wierzchołek odwrotny", czyli... on sam,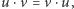 w związku z czym badane działanie jest przemienne.
w związku z czym badane działanie jest przemienne.
Przedstawione własności czynią z kostki dyskretnej z mnożeniem po współrzędnych grupę przemienną. Na skończonych (a także, ogólniej, lokalnie zwartych) grupach przemiennych można uprawiać analizę harmoniczną - jak zaraz zobaczymy, na kostce dyskretnej wystarczy do tego bardzo elementarny język.
Przyporządkujmy każdemu z wierzchołków liczbę rzeczywistą. Możemy oczywiście zrobić to na wiele różnych sposobów i każde takie przyporządkowanie jest niczym innym, jak funkcją określoną na kostce dyskretnej. Mając do dyspozycji dwie takie funkcje, 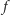 i
i 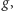 wprowadźmy ich iloczyn skalarny, czyli sumę iloczynów wartości tych funkcji, rozciągającą się po wszystkich
wprowadźmy ich iloczyn skalarny, czyli sumę iloczynów wartości tych funkcji, rozciągającą się po wszystkich 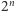 wierzchołkach:
wierzchołkach:
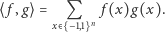 |
Każdy wierzchołek ma 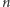 współrzędnych, więc dla każdego
współrzędnych, więc dla każdego 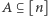 możemy rozpatrzyć funkcję, która wierzchołkowi przyporządkowuje iloczyn współrzędnych o wskaźnikach ze zbioru
możemy rozpatrzyć funkcję, która wierzchołkowi przyporządkowuje iloczyn współrzędnych o wskaźnikach ze zbioru 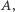 tzn. funkcję
tzn. funkcję
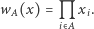 |
Przyjmujemy ponadto 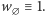 Oczywiście, funkcji tych jest dokładnie tyle co podzbiorów
Oczywiście, funkcji tych jest dokładnie tyle co podzbiorów ![|[n],](/math/temat/matematyka/analiza/2016/03/22/Analiza_na_kostce_dyskretnej/10x-61fc7624ac8e8cbcb1de55f16d8867cad7386d86-im-33,33,33-FF,FF,FF.gif) czyli
czyli 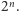 Dla
Dla 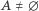 mamy
mamy
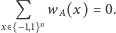 |
(1) |
Aby się o tym przekonać, wybierzmy dowolną liczbę 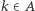 i zauważmy, że
i zauważmy, że

zatem składniki sumy (1) można pogrupować w "anulujące się" pary. Dla dowolnych 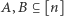 i dowolnego wierzchołka
i dowolnego wierzchołka 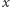 mamy też
mamy też
gdzie 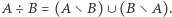 Równości (1) oraz (2) pozwalają łatwo sprawdzić, że jeśli
Równości (1) oraz (2) pozwalają łatwo sprawdzić, że jeśli 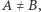 to
to 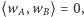 a
a 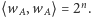 Funkcje
Funkcje 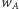 dla
dla 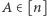 tworzą zatem układ ortogonalny. Nietrudno udowodnić, że jest to układ zupełny, tzn. każdą funkcję
tworzą zatem układ ortogonalny. Nietrudno udowodnić, że jest to układ zupełny, tzn. każdą funkcję 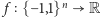 można w dokładnie jeden sposób przedstawić w postaci sumy
można w dokładnie jeden sposób przedstawić w postaci sumy 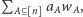 gdzie
gdzie ![|[n] = {1,2,...,n},](/math/temat/matematyka/analiza/2016/03/22/Analiza_na_kostce_dyskretnej/27x-61fc7624ac8e8cbcb1de55f16d8867cad7386d86-im-33,33,33-FF,FF,FF.gif) zaś
zaś 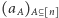 są współczynnikami rzeczywistymi. Sumy takie, zwane rozwinięciami Fouriera-Walsha, pełnią na kostce dyskretnej rolę zbliżoną do tej, którą w klasycznej analizie harmonicznej odgrywają rozwinięcia funkcji okresowych w trygonometryczne szeregi Fouriera, tj. szeregi postaci
są współczynnikami rzeczywistymi. Sumy takie, zwane rozwinięciami Fouriera-Walsha, pełnią na kostce dyskretnej rolę zbliżoną do tej, którą w klasycznej analizie harmonicznej odgrywają rozwinięcia funkcji okresowych w trygonometryczne szeregi Fouriera, tj. szeregi postaci 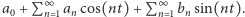 Nieco więcej na ten temat można przeczytać w [1].
Nieco więcej na ten temat można przeczytać w [1].
Wśród funkcji określonych na kostce dyskretnej szczególne zainteresowanie budzą w ostatnich latach funkcje przyjmujące tylko wartości 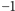 i
i 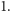 Każdą funkcję
Każdą funkcję 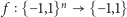 można bowiem naturalnie utożsamić z podzbiorem
można bowiem naturalnie utożsamić z podzbiorem 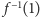 zbioru wszystkich podzbiorów zbioru
zbioru wszystkich podzbiorów zbioru ![|[n].](/math/temat/matematyka/analiza/2016/03/22/Analiza_na_kostce_dyskretnej/5x-b504898a1e55c8959ab756ccb973bb88e1173e10-im-33,33,33-FF,FF,FF.gif) To jednoznaczne przyporządkowanie przydaje się w badaniu zagadnień kombinatorycznych, natomiast z punktu widzenia informatyki teoretycznej ciekawsze jest rozumienie
To jednoznaczne przyporządkowanie przydaje się w badaniu zagadnień kombinatorycznych, natomiast z punktu widzenia informatyki teoretycznej ciekawsze jest rozumienie 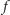 jako procedury, która z
jako procedury, która z  bitów danych wejściowych (input) tworzy jeden bit wyniku, co odpowiada rozmaitym procesom decyzyjnym czy klasyfikacyjnym. O przydatności tego typu rozważań pisał w Delcie 4/2015 Andrzej Dąbrowski. Badaniem funkcji
bitów danych wejściowych (input) tworzy jeden bit wyniku, co odpowiada rozmaitym procesom decyzyjnym czy klasyfikacyjnym. O przydatności tego typu rozważań pisał w Delcie 4/2015 Andrzej Dąbrowski. Badaniem funkcji 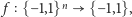 które bliskie są funkcjom afinicznym, zajmujemy się również na Wydziale Matematyki, Informatyki i Mechaniki UW ([2]).
które bliskie są funkcjom afinicznym, zajmujemy się również na Wydziale Matematyki, Informatyki i Mechaniki UW ([2]).