Myśl logarytmicznie!
W tym artykule ilustrujemy potęgę logarytmów w projektowaniu efektywnych algorytmów i obliczeń. Myślenie, w tle którego stoi logarytm, ukryty lub widoczny, nazwaliśmy myśleniem logarytmicznym. Stanowi ono jedną z podstawowych kompetencji niezbędnych przy efektywnym rozwiązywaniu rzeczywistych problemów informatycznych. Pokazujemy również - co może być ciekawe dla nauczycieli matematyki - jak wprowadzić pojęcie logarytmu, nie odwołując się do matematycznego formalizmu, a posługując się koncepcyjnym modelem redukcji rozmiaru problemu w każdym (lub w co drugim) kroku co najmniej o połowę. Może Cię zdziwić, że ta idea prowadząca do logarytmu występuje w algorytmie Euklidesa, który został opisany niemal 2000 lat przed wynalezieniem logarytmu przez Napiera.
Krótko po wynalezieniu logarytmu Edmund Gunter w 1620 roku utworzył skalę logarytmiczną, a z połączenia dwóch takich skal William Oughtred w 1622 roku zbudował suwak logarytmiczny. Oryginalnie, suwaki służyły do wykonywania mnożenia (patrz Rys. 1) i dzielenia, inne skale na suwakach służą do podnoszenia do kwadratu i do wyciągania pierwiastków kwadratowych, do obliczania trzecich potęg i pierwiastków trzeciego stopnia, do obliczania wartości funkcji trygonometrycznych i do wielu innych obliczeń. Jeden z najbogatszych suwaków, Faber Castell 2/83N, zawiera aż 21 skal. Budowano suwaki podłużne, okrągłe i ze skalami nawiniętymi na cylindry, by móc wydłużyć ich długości dla osiągnięcia dokładniejszych wyników - skala na cylindrycznym suwaku Fullera ma długość 12 metrów.
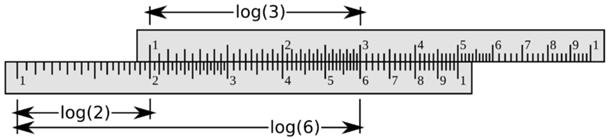
Rys. 1 Sposób obliczania iloczynu 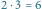 za pomocą suwaka logarytmicznego
za pomocą suwaka logarytmicznego
Dodajmy tutaj, że Napier wynalazł również tak zwane pałeczki Napiera, które służą do mnożenia liczb, nie mają one jednak nic wspólnego z logarytmami. Posłużyły natomiast Wilhelmowi Schickardowi do zbudowania w 1624 roku pierwszego kalkulatora mechanicznego.
Rok 1972 to początek agonii suwaków - zaczęły je wypierać stworzone z ich pomocą kalkulatory elektroniczne. Ponad 40 milionów wcześniej wyprodukowanych suwaków stało się nagle bezużytecznych i obecnie stanowi głównie eksponaty kolekcjonerskie. Dzisiaj jednak nie można wyobrazić sobie zajmowania się informatyką, bez przynajmniej "otarcia" się o logarytmy, co ilustrujemy w tym artykule.
Funkcje nie są obiektami matematycznymi lubianymi przez uczniów, zwłaszcza gdy są wprowadzane w sposób formalny jako przekształcenia (odwzorowania). Wśród nich "najgorszą sławą" cieszy się logarytm, bo nie dość, że jest to funkcja, to na dodatek jest to funkcja odwrotna. Jednakże do zrozumienia tego, o czym tutaj piszemy, nie będzie potrzebna znajomość pojęcia logarytmu.
W przeszłości uzasadnieniem dla posługiwania się logarytmami, były właściwości, które legły u podstaw jego wprowadzenia do obliczeń. Logarytm ułatwia wykonywanie złożonych obliczeń dzięki zastąpieniu działań multiplikatywnych (takich jak mnożenie i dzielenie) przez działania addytywne (dodawanie i odejmowanie). Nie tak dawno jeszcze, w szkołach posługiwano się tablicami logarytmicznymi, a na uczelniach i w zakładach pracy przyszli i zawodowi inżynierowie korzystali z suwaków logarytmicznych. Obecnie logarytm pełni rolę tzw. mental tool - narzędzia myślowego, sposobu rozumowania.
Rozważmy pięć następujących pytań:
- Ile należy przejrzeć kartek w słowniku, aby znaleźć poszukiwane hasło?
- Ile miejsca w komputerze (a dokładniej ile bitów) zajmuje liczba naturalna?
- Jak szybko można wykonywać potęgowanie dla dużych wykładników potęg?
- Ile trwa obliczanie największego wspólnego dzielnika dwóch liczb za pomocą algorytmu Euklidesa?
- Ile kroków wykonuje algorytm typu dziel i zwyciężaj uruchomiony na danych o
 elementach?
elementach?
Wspólną cechą odpowiedzi na te pytania jest to, że nie można ich udzielić, nie dotykając logarytmu, pośrednio lub bezpośrednio, a ponadto wyjaśnienie tych odpowiedzi służy lepszemu zrozumieniu pojęcia logarytmu i jego roli w projektowaniu efektywnych algorytmów.
Znajdź szybko hasło w słowniku, odgadnij ukrytą liczbę
Papierowa książka telefoniczna ma 1000 stron. Jak znaleźć numer telefonu do pana Skarbka, aby przeglądnąć możliwie najmniejszą liczbę stron w tej książce? Zapewne szybko wpadniesz na pomysł, że najlepszą metodą jest podział pliku stron, na których może być numer telefonu pana Skarbka, na połowę i odrzucenie tej połowy, w której na pewno nie ma informacji o panu Skarbku. Ten podział jest kontynuowany, aż pozostanie tylko jedna strona, na której może się znaleźć numer telefonu pana Skarbka. Jest to tak zwane poszukiwanie binarne lub przez połowienie.
W dwuosobowej grze w odgadywanie liczby z podanego przedziału, pomyślanej przez jedną z osób, w której druga osoba może zadawać pytania "czy pomyślana liczba jest większa czy mniejsza niż  " również możemy zastosować podobną strategię. Jeśli każde pytanie będzie dotyczyło wartości
" również możemy zastosować podobną strategię. Jeśli każde pytanie będzie dotyczyło wartości 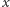 leżącej w połowie aktualnego przedziału, w którym znajduje się poszukiwana liczba, to liczba pytań niezbędna do odgadnięcia pomyślanej liczby będzie równa liczbie połowień oryginalnego przedziału.
leżącej w połowie aktualnego przedziału, w którym znajduje się poszukiwana liczba, to liczba pytań niezbędna do odgadnięcia pomyślanej liczby będzie równa liczbie połowień oryginalnego przedziału.
Przy okazji warto zwrócić uwagę na następujące kwestie:
- Bardzo ważny jest alfabetyczny porządek nazwisk w książce telefonicznej i liczb w przedziale. Jak ci się wydaje, ile stron należałoby przejrzeć w 1000-stronicowej książce telefonicznej, by znaleźć nazwisko właściciela telefonu o numerze 1234567?
- W przypadku słownika, w którym chcemy znaleźć hasło zaczynające się początkową literą alfabetu, na ogół próbujemy znaleźć poszukiwane hasło na początkowych stronach słownika. Taka metoda nazywa się interpolacyjnym poszukiwaniem - na ogół działa szybciej, niż binarne poszukiwanie (więcej na ten temat znajdziesz w książce M.M. Sysło, Algorytmy, WSiP 1997; Helion 2014).
Binarna reprezentacja liczb i rozmiar liczby w komputerze
Zapewne wiesz, jak otrzymać binarną reprezentację liczby naturalnej 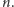 Taka reprezentacja jest generowana w trakcie podziału liczby
Taka reprezentacja jest generowana w trakcie podziału liczby 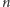 i otrzymywanych ilorazów przez 2. Rozpoczynamy od podzielenia
i otrzymywanych ilorazów przez 2. Rozpoczynamy od podzielenia 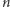 przez 2 i resztę z tego dzielenia
przez 2 i resztę z tego dzielenia  (0 lub 1) przyjmujemy za najmniej znaczący bit w reprezentacji. Następnie powtarzamy tę procedurę dla ilorazu
(0 lub 1) przyjmujemy za najmniej znaczący bit w reprezentacji. Następnie powtarzamy tę procedurę dla ilorazu 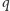 tak długo, jak długo iloraz
tak długo, jak długo iloraz 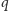 jest większy od 0. Na przykład, dla
jest większy od 0. Na przykład, dla 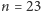 otrzymujemy
otrzymujemy 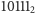 jak w tabeli 2.
jak w tabeli 2.
Czy zastanawiałeś się, z ilu bitów składa się binarna reprezentacja dziesiętnej liczby naturalnej 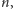 lub inaczej, jak dużą pamięć w komputerze zajmuje liczba
lub inaczej, jak dużą pamięć w komputerze zajmuje liczba 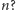 By odpowiedzieć na to pytanie, załóżmy, że
By odpowiedzieć na to pytanie, załóżmy, że  zajmuje
zajmuje 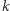 bitów i określmy, jaka jest najmniejsza i największa liczba zajmująca dokładnie
bitów i określmy, jaka jest najmniejsza i największa liczba zajmująca dokładnie 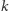 bitów. Największa taka liczba składa się z
bitów. Największa taka liczba składa się z 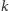 bitów równych 1, czyli
bitów równych 1, czyli

Z drugiej strony, najmniejsza liczba reprezentowana dokładnie na 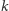 bitach ma tylko jedną jedynkę na najbardziej znaczącej pozycji. Stąd otrzymujemy następujące nierówności:
bitach ma tylko jedną jedynkę na najbardziej znaczącej pozycji. Stąd otrzymujemy następujące nierówności:

Dodajmy 1 do wszystkich stron tych nierówności i weźmy logarytm 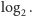 Otrzymamy:
Otrzymamy:

Ponieważ liczba bitów 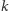 jest liczbą naturalną (całkowitą dodatnią), mamy:
jest liczbą naturalną (całkowitą dodatnią), mamy:

gdzie 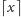 jest sufitem liczby
jest sufitem liczby 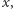 czyli równa się najmniejszej liczbie naturalnej większej lub równej
czyli równa się najmniejszej liczbie naturalnej większej lub równej 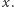 Z tej części rozważań możemy wyciągnąć wniosek, że naturalna liczba
Z tej części rozważań możemy wyciągnąć wniosek, że naturalna liczba  zajmuje w pamięci komputera około
zajmuje w pamięci komputera około 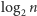 bitów - ta liczba jest często przyjmowana za komputerowy rozmiar liczby
bitów - ta liczba jest często przyjmowana za komputerowy rozmiar liczby  Zauważmy, że poszukiwanie binarne w przedziale zawierającym
Zauważmy, że poszukiwanie binarne w przedziale zawierającym  liczb odpowiada tworzeniu binarnej reprezentacji liczby
liczb odpowiada tworzeniu binarnej reprezentacji liczby 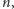 liczba kroków w takim poszukiwaniu wynosi około
liczba kroków w takim poszukiwaniu wynosi około 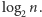
Możemy teraz algorytmicznie zdefiniować 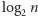 jako:
jako:
Definicja. Logarytm 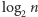 jest równy liczbie kroków, jakie potrzebujemy by zmniejszyć
jest równy liczbie kroków, jakie potrzebujemy by zmniejszyć 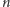 do
do 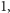 dzieląc sukcesywnie przez
dzieląc sukcesywnie przez 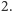
O znaczeniu i "potędze" logarytmów i funkcji logarytmicznej w informatyce, a ogólniej - w obliczeniach decyduje szybkość wzrostu jej wartości, nieporównywalnie mała względem szybkości wzrostu jej argumentu, co ilustrujemy w tabeli 3. A zatem dla liczb, które mają około stu cyfr, wartość logarytmu wynosi tylko około 333.
Szybkie podnoszenie do potęgi
Podnoszenie do potęgi jest bardzo prostym, szkolnym zadaniem. Na przykład, aby obliczyć 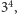 wykonujemy trzy mnożenia
wykonujemy trzy mnożenia 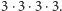 A zatem w ogólności, aby w ten sposób obliczyć wartość potęgi
A zatem w ogólności, aby w ten sposób obliczyć wartość potęgi 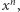 należy wykonać
należy wykonać 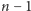 mnożeń: o jedno mniej niż wynosi wykładnik potęgi. Czy ten "szkolny" algorytm jest na tyle szybki, by obliczyć na przykład wartość potęgi:
mnożeń: o jedno mniej niż wynosi wykładnik potęgi. Czy ten "szkolny" algorytm jest na tyle szybki, by obliczyć na przykład wartość potęgi:

która może pojawić się przy szyfrowaniu metodą RSA informacji przesyłanych w Internecie?
Oszacujmy, ile czasu będzie trwało obliczanie tej potęgi, jeśli zastosujemy szkolny algorytm, czyli ile czasu zabierze wykonanie  mnożeń. Przypuśćmy, że dysponujemy superkomputerem, który działa z szybkością jednego petaflopa, zatem wykonuje około
mnożeń. Przypuśćmy, że dysponujemy superkomputerem, który działa z szybkością jednego petaflopa, zatem wykonuje około 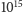 operacji na sekundę. Obliczenie powyższej potęgi będzie trwało
operacji na sekundę. Obliczenie powyższej potęgi będzie trwało

Jeśli taki algorytm byłby stosowany do szyfrowania naszej poczty w Internecie, to nigdy nie otrzymalibyśmy żadnego listu. Dodajmy, że w praktycznych sytuacjach konieczne jest obliczanie potęg o wykładnikach, które mają kilkaset cyfr.
Postaramy się teraz tak wykonywać potęgowanie, aby w każdym kroku wykładnik zmniejszył się około o połowę. W tym celu zauważmy, że jeżeli  jest liczba parzystą, czyli na przykład
jest liczba parzystą, czyli na przykład 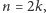 to
to 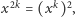 a gdy
a gdy  jest liczbą nieparzystą, czyli
jest liczbą nieparzystą, czyli 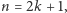 to
to 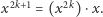 Na przykład, by obliczyć wartość
Na przykład, by obliczyć wartość 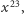 postępujemy następująco:
postępujemy następująco:

Zatem wartość potęgi 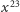 może być obliczona przy użyciu 7 mnożeń (podnoszenie do kwadratu to jedno mnożenie).
może być obliczona przy użyciu 7 mnożeń (podnoszenie do kwadratu to jedno mnożenie).
Oszacujmy, ile mnożeń jest wykonywanych w takim algorytmie dla dowolnego 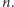 W tym celu porównajmy binarną reprezentację liczby
W tym celu porównajmy binarną reprezentację liczby 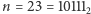 z kolejnością wykonywania mnożeń w tym algorytmie, patrząc od prawej do lewej. Nietrudno się przekonać, że z wyjątkiem najbardziej znaczącej pozycji w reprezentacji binarnej wykładnika
z kolejnością wykonywania mnożeń w tym algorytmie, patrząc od prawej do lewej. Nietrudno się przekonać, że z wyjątkiem najbardziej znaczącej pozycji w reprezentacji binarnej wykładnika 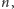 każdemu bitowi o wartości 1 odpowiada mnożenie przez
każdemu bitowi o wartości 1 odpowiada mnożenie przez 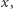 a każdej pozycji odpowiada podniesienie do kwadratu. A zatem, liczba mnożeń potrzebnych do obliczenia wartości
a każdej pozycji odpowiada podniesienie do kwadratu. A zatem, liczba mnożeń potrzebnych do obliczenia wartości 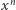 za pomocą powyższego algorytmu jest równa liczbie pozycji w binarnej reprezentacji liczby
za pomocą powyższego algorytmu jest równa liczbie pozycji w binarnej reprezentacji liczby 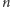 minus 1 plus liczba bitów równych 1 w tej reprezentacji także minus 1. Ponieważ, jak wiemy, długość reprezentacji binarnej liczby
minus 1 plus liczba bitów równych 1 w tej reprezentacji także minus 1. Ponieważ, jak wiemy, długość reprezentacji binarnej liczby 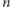 wynosi około
wynosi około 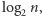 liczba mnożeń potrzebnych do obliczenia wartości
liczba mnożeń potrzebnych do obliczenia wartości 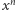 wynosi około
wynosi około 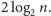
Sprawdźmy, jaki to da efekt, gdy 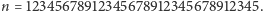 W tym przypadku
W tym przypadku 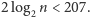 Zatem zamiast czekać
Zatem zamiast czekać 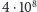 lat, wynik możemy otrzymać wykonując nie więcej niż
lat, wynik możemy otrzymać wykonując nie więcej niż 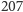 mnożeń! To szokujące osiągnięcie naszego algorytmu! Na podstawie tabeli 3 widać, że obliczenie wartości
mnożeń! To szokujące osiągnięcie naszego algorytmu! Na podstawie tabeli 3 widać, że obliczenie wartości 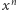 dla
dla  z setkami cyfr wymaga wykonania kilka tysięcy mnożeń, co na zwykłym komputerze trwa ułamek sekundy.
z setkami cyfr wymaga wykonania kilka tysięcy mnożeń, co na zwykłym komputerze trwa ułamek sekundy.
Przedstawiony algorytm można zapisać w postać rekurencyjnej:

Algorytmy potęgowania są dobitną ilustracją słów Ralpha Gomory'ego, naukowego szefa firmy IBM: Najlepszym sposobem przyspieszania pracy komputerów jest obarczanie ich mniejszą liczba działań. Czyli prawdziwe przyspieszanie obliczeń osiągamy dzięki efektywnym algorytmom, a nie szybszym komputerom, a w tym konkretnym przypadku, dzięki zastąpieniu algorytmu liniowego przez algorytm o złożoności logarytmicznej.

Rys. 5 Geometryczne uzasadnienie faktu, że reszta z dzielenia  przez
przez 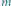 jest nie większa niż
jest nie większa niż 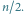
Algorytm Euklidesa a metoda połowienia
Okazuje się, że Euklides był bliski wynalezienia logarytmu, niemal 2000 lat przed tym, jak zrobił to John Napier. Algorytm Euklidesa jest jednym z najstarszych znanych algorytmów. Służy do znajdowania największego wspólnego dzielnika (w skrócie 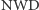 ) dwóch liczb. W tabeli 4 są zamieszczone wyniki obliczeń tego algorytmu w trakcie znajdowania
) dwóch liczb. W tabeli 4 są zamieszczone wyniki obliczeń tego algorytmu w trakcie znajdowania 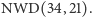 W ogólności, algorytm Euklidesa generuje następujący ciąg reszt (trzecia kolumna w tabeli 4):
W ogólności, algorytm Euklidesa generuje następujący ciąg reszt (trzecia kolumna w tabeli 4):

Te reszty są generowane zgodnie z następującym ciągiem równości:

i ostatecznie 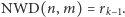
Pierwsza równość odpowiada pierwszemu wierszowi w tabeli 4, a ostatnia - ostatniemu wierszowi. Ilorazy 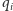 i reszty
i reszty 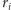 w tych równościach spełniają równości:
w tych równościach spełniają równości:

Powstaje teraz pytanie, ile kroków wykonuje algorytm Euklidesa, by obliczyć wartość 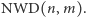 Pewna sugestia może wyniknąć z porównania liczb w pierwszej i trzeciej kolumnie w tabeli 4. Można zauważyć, że w każdym wierszu liczba w trzeciej kolumnie jest co najmniej dwa razy mniejsza niż liczba w pierwszej kolumnie, a zatem reszta
Pewna sugestia może wyniknąć z porównania liczb w pierwszej i trzeciej kolumnie w tabeli 4. Można zauważyć, że w każdym wierszu liczba w trzeciej kolumnie jest co najmniej dwa razy mniejsza niż liczba w pierwszej kolumnie, a zatem reszta 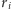 w równaniu
w równaniu 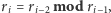 jest co najmniej dwa razy mniejsza niż
jest co najmniej dwa razy mniejsza niż 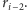
Uzasadnienie tego faktu jest bardzo proste, jeśli posłużymy się rozumowaniem geometrycznym (Rys. 5).
A zatem, chcemy pokazać, że reszta  z dzielenia
z dzielenia  przez
przez 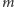 nie jest większa niż
nie jest większa niż 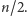 Rozważmy dwa przypadki:
Rozważmy dwa przypadki:
- (a)
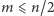 - ponieważ reszta nie jest większa niż
- ponieważ reszta nie jest większa niż 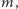 więc wynosi co najwyżej
więc wynosi co najwyżej 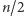 ;
;- (b)
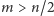 - reszta wynosi
- reszta wynosi 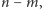 a
a 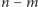 nie jest większe niż
nie jest większe niż 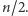
A zatem, w ciągu reszt generowanym w algorytmie Euklidesa każda reszta jest co najmniej dwa razy mniejsza niż reszta, która występuje w tym ciągu o dwie pozycje wcześniej. Przypomina to ciąg liczb generowany przez algorytm poszukiwania binarnego, z wyjątkiem tego, że generowany ciąg może być w najgorszym przypadku dwa razy dłuższy. Ważnym wnioskiem jest więc stwierdzenie, że:
Twierdzenie. Algorytm Euklidesa oblicza 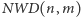 dla
dla 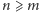 w co najwyżej
w co najwyżej 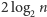 krokach.
krokach.
Pewnym wyzwaniem jest pytanie dla jakich liczb 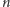 i
i 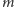 algorytm Euklidesa wykonuje największą możliwą liczbę kroków (dwie takie liczby zostały użyte w naszym przykładzie). Odpowiedź może być zaskakująca.
algorytm Euklidesa wykonuje największą możliwą liczbę kroków (dwie takie liczby zostały użyte w naszym przykładzie). Odpowiedź może być zaskakująca.
Liczby Fibonacciego
Tendencja do zastępowania algorytmów o złożoności liniowej przez algorytmy o złożoności logarytmicznej, zilustrowana algorytmem szybkiego potęgowaniem, występuje w wielu innych problemach algorytmicznych, np. przy wyznaczaniu wartości liczb Fibonacciego. Klasyczna zależność rekurencyjna, definiująca liczby Fibonacciego, może być wykorzystana do podania algorytmu liniowego, który dodatkowo unika wielokrotnych, takich samych odwołań rekurencyjnych.
Aby otrzymać w tym przypadku algorytm o złożoności logarytmicznej, należy posłużyć się układem dwóch zależności rekurencyjnych, w których indeksy liczb Fibonacciego po prawej stronie są redukowane o około połowę. I ponownie, jak powyżej, by uniknąć wielokrotnych takich samych wywołań rekurencyjnych, należy rekurencję zrealizować jako iterację.

Więcej na ten temat można znaleźć w książce M.M. Sysło, Piramidy, szyszki i inne konstrukcje algorytmiczne, WSiP 1998; Helion 2015.
Metody podziału i ograniczeń
Wszystkie algorytmy zaprezentowane w tej pracy bazują na idei metody dziel i zwyciężaj. W informatyce istnieje bardzo wiele algorytmów będących realizacją tej idei. We wszystkich przypadkach to podejście algorytmiczne wprowadza do ogólnego wyrażenia na złożoność obliczeniową rozwiązywanego problemu jedynie logarytmiczny czynnik. Tak jest na przykład w przypadku sortowania przez binarne umieszczanie czy sortowanie przez scalanie.
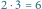 za pomocą suwaka logarytmicznego
za pomocą suwaka logarytmicznego przez
przez 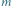 jest nie większa niż
jest nie większa niż