Analiza, Dedekind i Cantor
Sztuka w trzech aktach z prologiem i epilogiem...
Prolog
Rzecz dotyczy pytania: na ile Dedekind jest potrzebny Analizie?
Akt I.
Zawiązanie akcji, czyli co to jest Analiza i co ma z tym wspólnego Dedekind; pojawienie się Cantora.
Ciało 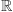 liczb rzeczywistych, które poznajemy (a raczej powinniśmy poznać) w szkole średniej, jest opisane pewnym układem aksjomatów. Aksjomaty te można podzielić na dwie klasy; pierwszą klasę stanowią wszystkie aksjomaty z wyjątkiem jednego - tzw. Aksjomatu Dedekinda. Aksjomaty pierwszej klasy mają charakter arytmetyczno-porządkowy. Mówią one m.in., że działania arytmetyczne na liczbach rzeczywistych są łączne, przemienne, że odejmowanie jest wykonalne zawsze, a dzielenie - tylko przez liczby różne od 0; że mnożenie jest rozdzielne względem dodawania; że dodawanie i mnożenie przez liczby dodatnie zachowują porządek (tzn. nierówności) itd. Cechą wspólną tych aksjomatów jest to, że mówią one o własnościach liczb rzeczywistych. Zupełnie inny charakter ma Aksjomat Dedekinda. Opisuje on pewną własność podzbiorów liczb rzeczywistych.
liczb rzeczywistych, które poznajemy (a raczej powinniśmy poznać) w szkole średniej, jest opisane pewnym układem aksjomatów. Aksjomaty te można podzielić na dwie klasy; pierwszą klasę stanowią wszystkie aksjomaty z wyjątkiem jednego - tzw. Aksjomatu Dedekinda. Aksjomaty pierwszej klasy mają charakter arytmetyczno-porządkowy. Mówią one m.in., że działania arytmetyczne na liczbach rzeczywistych są łączne, przemienne, że odejmowanie jest wykonalne zawsze, a dzielenie - tylko przez liczby różne od 0; że mnożenie jest rozdzielne względem dodawania; że dodawanie i mnożenie przez liczby dodatnie zachowują porządek (tzn. nierówności) itd. Cechą wspólną tych aksjomatów jest to, że mówią one o własnościach liczb rzeczywistych. Zupełnie inny charakter ma Aksjomat Dedekinda. Opisuje on pewną własność podzbiorów liczb rzeczywistych.
Mianowicie:
Aksjomat (Dedekinda). Każdy ograniczony podzbiór liczb rzeczywistych ma kres górny.
Nieco trudniej jest powiedzieć, co to jest Analiza. Najlepsze określenie, jakie potrafię wymyślić, jest następujące: Analiza jest to zbiór twierdzeń, dających się wyprowadzić z aksjomatów ciała liczb rzeczywistych, opisujących pewne własności funkcji o wartościach rzeczywistych określonych na podzbiorach liczb rzeczywistych.
Najłatwiej wyjaśnić, o jakie własności tutaj chodzi, na przykładzie dwóch podstawowych twierdzeń Analizy.
Twierdzenie 1 (Darboux). Jeżeli funkcja ciągła 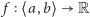 przyjmuje na końcach przedziału
przyjmuje na końcach przedziału 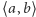 wartości różnych znaków, to wewnątrz przedziału istnieje taka liczba
wartości różnych znaków, to wewnątrz przedziału istnieje taka liczba 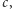 że
że 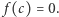
Twierdzenie 2 (Lagrange). Jeżeli funkcja ciągła 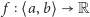 jest różniczkowalna wewnątrz przedziału
jest różniczkowalna wewnątrz przedziału 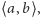 to wewnątrz tego przedziału istnieje taki punkt
to wewnątrz tego przedziału istnieje taki punkt  że
że 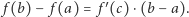
Zanotujmy jeszcze jedno twierdzenie Analizy.
Twierdzenie 3 (Cantor). Ciało liczb rzeczywistych nie jest przeliczalne.
Akt II.
Czy wszystkie liczby rzeczywiste są rzeczywiście potrzebne, czyli tragiczny koniec Analizy.
Żeby zobaczyć, co się stanie z Analizą, kiedy zabraknie Aksjomatu Dedekinda, weźmy dowolne mniejsze podciało 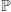 ciała liczb rzeczywistych, tzn. taki zbiór liczb, w którym spełnione są wszystkie aksjomaty należące do pierwszej klasy. Ponieważ
ciała liczb rzeczywistych, tzn. taki zbiór liczb, w którym spełnione są wszystkie aksjomaty należące do pierwszej klasy. Ponieważ 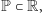 więc istnieje
więc istnieje 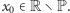 Niech
Niech  i
i  będą takimi liczbami rzeczywistymi należącymi do
będą takimi liczbami rzeczywistymi należącymi do 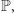 że
że 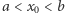 (takie liczby muszą istnieć!). Niech
(takie liczby muszą istnieć!). Niech 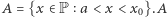 jest zbiorem ograniczonym. W ciele
jest zbiorem ograniczonym. W ciele 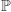 nie jest spełniony Aksjomat Dedekinda, gdyż z tego, że
nie jest spełniony Aksjomat Dedekinda, gdyż z tego, że 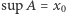 i
i 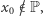 wynika, iż w ciele
wynika, iż w ciele 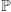 zbiór
zbiór  nie ma kresu górnego. Gdyby Twierdzenia Analizy nie zależały od Aksjomatu Dedekinda, tzn. dawały się wyprowadzić z aksjomatów należących do pierwszej klasy, to ponieważ
nie ma kresu górnego. Gdyby Twierdzenia Analizy nie zależały od Aksjomatu Dedekinda, tzn. dawały się wyprowadzić z aksjomatów należących do pierwszej klasy, to ponieważ  spełnia wszystkie aksjomaty należące do pierwszej klasy, byłyby one prawdziwe dla funkcji określonych na podzbiorach
spełnia wszystkie aksjomaty należące do pierwszej klasy, byłyby one prawdziwe dla funkcji określonych na podzbiorach 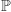 o wartościach w
o wartościach w 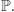 Tak jednak nie jest. Np. określmy funkcję
Tak jednak nie jest. Np. określmy funkcję 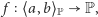 gdzie
gdzie 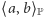 oznacza odcinek domknięty w
oznacza odcinek domknięty w  tzn.
tzn.  wzorem
wzorem

Łatwo można zauważyć, że spełnia ona założenia twierdzeń 1 i 2, natomiast tezy tych twierdzeń nie zachodzą. Z definicji 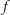 wynika, że
wynika, że  dla każdego
dla każdego 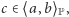 także teza twierdzenia 2 nie może zachodzić, gdyż
także teza twierdzenia 2 nie może zachodzić, gdyż 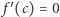 dla każdego
dla każdego 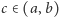 i
i 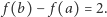
Ponieważ cała nasza konstrukcja wynikła z faktu, że istnieje  z rozważań powyższych można wyciągnąć
z rozważań powyższych można wyciągnąć
Z drugiej strony można pokazać, że rezygnacja z Aksjomatu Dedekinda spowoduje nie tylko "zawalenie się" twierdzeń 1 i 2. Rezygnacja taka spowoduje tragiczny koniec Analizy - zawali się w niej praktycznie wszystko. Zostaną tylko nieciekawe ruiny.
Akt III.
Cudowne ocalenie Analizy, czyli liczby i funkcje definiowalne.
Całe nieszczęście wyniknęło z tego, że chcieliśmy z jednej strony zmniejszyć zbiór liczb w Analizie, a z drugiej strony - pozostawić zbiór funkcji praktycznie bez zmian. Zawalenia się Analizy można uniknąć, jeżeli odpowiedniemu zmniejszeniu zbioru liczb towarzyszy odpowiednie zmniejszenie zbioru funkcji. Oto jeden z takich sposobów. Niech  będzie podzbiorem liczb rzeczywistych, złożonym z liczb definiowalnych za pomocą działań arytmetycznych, liczb naturalnych, zbioru liczb naturalnych, indukcji i kresu górnego (tzn. z liczb, które można "konkretnie" zdefiniować za pomocą tych pojęć).
będzie podzbiorem liczb rzeczywistych, złożonym z liczb definiowalnych za pomocą działań arytmetycznych, liczb naturalnych, zbioru liczb naturalnych, indukcji i kresu górnego (tzn. z liczb, które można "konkretnie" zdefiniować za pomocą tych pojęć).
Łatwo można wykazać, że 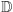 jest podciałem ciała liczb rzeczywistych. Np. żeby wykazać, że jeżeli
jest podciałem ciała liczb rzeczywistych. Np. żeby wykazać, że jeżeli 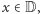 to
to 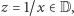 wystarczy zauważyć, iż liczbę
wystarczy zauważyć, iż liczbę  można zdefiniować następująco:
można zdefiniować następująco:
"  jest jedyną liczbą, taką że
jest jedyną liczbą, taką że 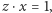 gdzie
gdzie 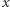 jest zdefiniowane przez..."
jest zdefiniowane przez..."
Ponieważ zbiór wszystkich "konkretnych" definicji jest przeliczalny, zatem ciało 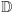 jest przeliczalne; a więc
jest przeliczalne; a więc  jest istotnie mniejsze niż ciało liczb rzeczywistych (por. twierdzenie 3).
jest istotnie mniejsze niż ciało liczb rzeczywistych (por. twierdzenie 3).
Umówmy się, że przez podzbiór ciała  będziemy rozumieli podzbiór
będziemy rozumieli podzbiór 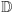 definiowalny za pomocą pojęcia "liczby definiowalne" i pojęć wymienionych wyżej. Można udowodnić, że dla ciała
definiowalny za pomocą pojęcia "liczby definiowalne" i pojęć wymienionych wyżej. Można udowodnić, że dla ciała  i jego podzbiorów (definiowalnych) spełniony jest Aksjomat Dedekinda, tj. każdy ograniczony podzbiór definiowalny w
i jego podzbiorów (definiowalnych) spełniony jest Aksjomat Dedekinda, tj. każdy ograniczony podzbiór definiowalny w 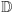 ma kres górny należący do
ma kres górny należący do 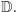
Wniosek 2. Ciało 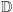 spełnia wszystkie aksjomaty ciała liczb rzeczywistych (przy interpretacji: podzbiór = podzbiór definiowalny).
spełnia wszystkie aksjomaty ciała liczb rzeczywistych (przy interpretacji: podzbiór = podzbiór definiowalny).
Rozważmy wszystkie funkcje definiowalne z 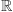 w
w 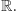
Dowód. Jeżeli  jest liczbą definiowalną, a
jest liczbą definiowalną, a 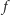 jest funkcją definiowalną, to definicja
jest funkcją definiowalną, to definicja  wygląda następująco:
wygląda następująco:
"  jest jedyną liczbą rzeczywistą, taką że
jest jedyną liczbą rzeczywistą, taką że 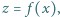 gdzie
gdzie  jest zdefiniowane przez..., a
jest zdefiniowane przez..., a  jest zdefiniowane przez...".
jest zdefiniowane przez...".
Zatem jeżeli ograniczymy się do liczb, podzbiorów i funkcji definiowalnych, to w otrzymanym modelu spełnione będą wszystkie aksjomaty ciała liczb rzeczywistych, a więc prawdziwe będą wszystkie twierdzenia Analizy (bo można je z tych aksjomatów wyprowadzić). Nazwijmy sobie tę teorię Analizą Definiowalną.
Wniosek 4. W obrębie Analizy Definiowalnej wszystkie twierdzenia Analizy są prawdziwe przy następującej interpretacji:

W szczególności, w obrębie Analizy Definiowalnej prawdziwe jest twierdzenie 3 (porównaj definicję zbioru przeliczalnego). To znaczy, że zachodzi
Epilog
Zaskakujące konsekwencje, czyli jak przeliczalność zbioru (i nie tylko ona) może zależeć od naszego obrazu świata.
Na początku aktu III stwierdziliśmy, że ciało 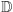 jest przeliczalne, na końcu zaś tego samego aktu podaliśmy twierdzenie Cantora mówiące, że ciało
jest przeliczalne, na końcu zaś tego samego aktu podaliśmy twierdzenie Cantora mówiące, że ciało 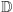 nie jest przeliczalne. Sprzeczność! Chcieliśmy ocalić Analizę, a w efekcie utopiliśmy Matematykę. Sprawa domaga się wyjaśnienia!
nie jest przeliczalne. Sprzeczność! Chcieliśmy ocalić Analizę, a w efekcie utopiliśmy Matematykę. Sprawa domaga się wyjaśnienia!
Wyjaśnienie takie jest stosunkowo proste. To, czy pewien zbiór 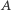 jest przeliczalny, czy nie, nie jest własnością absolutną tego zbioru. Może to w pewnych przypadkach zależeć od przyjętego obrazu (modelu) "świata". Mianowicie, w naszym przykładzie
jest przeliczalny, czy nie, nie jest własnością absolutną tego zbioru. Może to w pewnych przypadkach zależeć od przyjętego obrazu (modelu) "świata". Mianowicie, w naszym przykładzie
- w przypadku Analizy model zawierał dużo elementów i dużo funkcji - a więc nic dziwnego, że wśród nich znalazła się funkcja
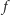 odwzorowująca zbiór liczb naturalnych na zbiór
odwzorowująca zbiór liczb naturalnych na zbiór 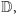 co spowodowało, że zbiór
co spowodowało, że zbiór 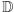 z punktu widzenia Analizy jest przeliczalny (porównaj definicję zbioru przeliczalnego),
z punktu widzenia Analizy jest przeliczalny (porównaj definicję zbioru przeliczalnego), - w przypadku Analizy Definiowalnej model zawierał mniej elementów i mniej funkcji; twierdzenie Cantora dla Analizy Definiowalnej orzeka, iż tych funkcji jest tak mało, że nie znajduje się wśród nich żadna funkcja odwzorowująca liczby naturalne na
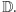
Ponieważ dodawanie jest "efektywnie" wykonalne, więc w każdym modelu analizy 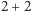 musi się równać
musi się równać  Natomiast przeliczalność zbioru nie jest efektywnie sprawdzalna. To znaczy - nie istnieje skończony algorytm pozwalający rozstrzygnąć, czy dany zbiór jest przeliczalny, czy nie. Zdarza się, że w przypadku takich nieefektywnych pojęć odpowiedź na pytanie zależy od przyjętego modelu świata. I tak właśnie jest z przeliczalnością zbioru
Natomiast przeliczalność zbioru nie jest efektywnie sprawdzalna. To znaczy - nie istnieje skończony algorytm pozwalający rozstrzygnąć, czy dany zbiór jest przeliczalny, czy nie. Zdarza się, że w przypadku takich nieefektywnych pojęć odpowiedź na pytanie zależy od przyjętego modelu świata. I tak właśnie jest z przeliczalnością zbioru 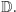 Podobnie nieefektywnym postulatem jest używany w Geometrii:
Podobnie nieefektywnym postulatem jest używany w Geometrii:
Aksjomat (Archimedesa). Odkładając wielokrotnie na prostej dany odcinek 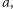 możemy uzyskać odcinek większy od danego odcinka
możemy uzyskać odcinek większy od danego odcinka 
I w tym przypadku odpowiedź na pytanie, czy tak jest naprawdę, zależy od przyjętego modelu Geometrii.
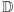
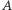 nazywamy taką najmniejszą liczbę rzeczywistą
nazywamy taką najmniejszą liczbę rzeczywistą 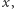 że dla każdego
że dla każdego 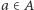 zachodzi
zachodzi 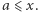 Kres górny zbioru
Kres górny zbioru 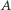 oznaczamy zwykle przez
oznaczamy zwykle przez 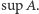
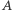 nazywa się przeliczalnym, jeżeli istnieje funkcja przekształcająca zbiór liczb naturalnych na ten zbiór.
nazywa się przeliczalnym, jeżeli istnieje funkcja przekształcająca zbiór liczb naturalnych na ten zbiór.