Konstrukcja, która zmieniła definicję krzywej
Na nieskończoności opierają się konstrukcje większości obiektów analizy matematycznej, choć często w niejawny sposób. Przyjrzyjmy się choćby ciągłości - pojęciu na pierwszy rzut oka z nieskończonością niezwiązanemu. Można powiedzieć, że funkcja jest ciągła, jeśli "nie rozrywa" dziedziny...
Jednak gdy chcemy ciągłość wyrazić precyzyjnie, chętnie sięgniemy do szufladki z nieskończonością, by posłużyć się pojęciem zbieżności i podać definicję:
Definicja. Funkcja ![| f [0,1] R2](/math/temat/matematyka/analiza/2013/06/28/Konstrukcja_ktora_zmienila_definicje/1x-3aa3db88a9012e1fc71cbc72762b10960e963309-im-33,33,33-FF,FF,FF.gif) jest ciągła w punkcie
jest ciągła w punkcie ![|t∈ [0,1],](/math/temat/matematyka/analiza/2013/06/28/Konstrukcja_ktora_zmienila_definicje/2x-3aa3db88a9012e1fc71cbc72762b10960e963309-im-33,33,33-FF,FF,FF.gif) jeśli
jeśli 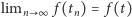 dla każdego ciągu
dla każdego ciągu 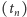 o wyrazach w
o wyrazach w ![[0,1]](/math/temat/matematyka/analiza/2013/06/28/Konstrukcja_ktora_zmienila_definicje/5x-3aa3db88a9012e1fc71cbc72762b10960e963309-im-33,33,33-FF,FF,FF.gif) zbieżnego do
zbieżnego do 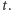
Powyższy przykład pokazuje, że nieskończoność może być użytecznym narzędziem przy budowaniu ścisłych definicji opartych na mniej precyzyjnych intuicjach. Czasem jednak, przez nieskończoność właśnie, rozsądna, zdawałoby się, definicja może okazać się nieodpowiednia.
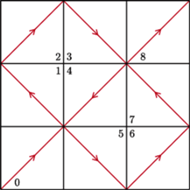
Rys. 1 Łamana 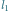 i kwadraty pierwszego podziału; poniżej krzywa odwiedzająca kwadraty w tej samej kolejności co
i kwadraty pierwszego podziału; poniżej krzywa odwiedzająca kwadraty w tej samej kolejności co 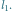

Rys. 2 Łamana 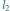 i kwadraty drugiego podziału.
i kwadraty drugiego podziału.

Spróbujmy zdefiniować krzywą na płaszczyźnie. Definicja powinna obejmować np. wykres funkcji kwadratowej, łamaną, czy tor ruchu punktu materialnego. Chcielibyśmy, by krzywa była obiektem ciągłym i jednowymiarowym, zatem naturalnie byłoby przyjąć, że krzywa to ciągły obraz odcinka. Taką też definicję zaproponował w XIX wieku Camille Jordan. Okazuje się jednak, że tak opisana klasa nie do końca odpowiada intuicjom związanym z pojęciem krzywej, gdyż należy do niej obiekt o dodatnim polu - istnieje bowiem funkcja ciągła, która przekształca odcinek ![|[0, 1]](/math/temat/matematyka/analiza/2013/06/28/Konstrukcja_ktora_zmienila_definicje/1x-7ad6b229b71d246ffb026fd8063721e6cdbd04ea-im-33,33,33-FF,FF,FF.gif) na kwadrat. Przykład takiej funkcji jako pierwszy podał Peano w 1890 roku.
na kwadrat. Przykład takiej funkcji jako pierwszy podał Peano w 1890 roku.
Jak skonstruować taką nietypową "krzywą"? Należy odpowiednio dobrać nieskończony ciąg funkcji ciągłych określonych na ![[0,1].](/math/temat/matematyka/analiza/2013/06/28/Konstrukcja_ktora_zmienila_definicje/1x-b3c6aa3ba6dfcfa2b8883061034a50e1bf925394-im-33,33,33-FF,FF,FF.gif) Obraz każdej z funkcji w ciągu jest łamaną o skończonej liczbie odcinków, jednak dopuszczenie do konstrukcji nieskończoności pod postacią przejścia granicznego prowadzi do funkcji, której obrazem jest pełen kwadrat.
Obraz każdej z funkcji w ciągu jest łamaną o skończonej liczbie odcinków, jednak dopuszczenie do konstrukcji nieskończoności pod postacią przejścia granicznego prowadzi do funkcji, której obrazem jest pełen kwadrat.
Przyjrzyjmy się dokładniej konstrukcji odpowiedniego ciągu funkcyjnego. Niech 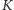 będzie kwadratem o boku 1. Kwadrat
będzie kwadratem o boku 1. Kwadrat 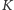 dzielimy na
dzielimy na 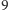 przystających kwadratów, które numerujemy od 0 do 8 (kwadrat o numerze
przystających kwadratów, które numerujemy od 0 do 8 (kwadrat o numerze 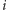 oznaczamy
oznaczamy 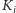 ), następnie tworzymy łamaną
), następnie tworzymy łamaną 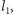 której odcinkami są wybrane przekątne kolejnych kwadratów (patrz Rys. 1). Funkcja
której odcinkami są wybrane przekątne kolejnych kwadratów (patrz Rys. 1). Funkcja ![f [0,1] K 1](/math/temat/matematyka/analiza/2013/06/28/Konstrukcja_ktora_zmienila_definicje/7x-9be2887f1510a040249654b274bb71f5769fd191-im-33,33,33-FF,FF,FF.gif) opisuje położenie w chwili
opisuje położenie w chwili 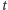 punktu poruszającego się po łamanej zgodnie z zadanym przez strzałki na rysunku kierunkiem i stałą prędkością równą
punktu poruszającego się po łamanej zgodnie z zadanym przez strzałki na rysunku kierunkiem i stałą prędkością równą 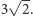 Zanotujmy jeszcze, że gdy
Zanotujmy jeszcze, że gdy ![t ∈[i9, i+91],](/math/temat/matematyka/analiza/2013/06/28/Konstrukcja_ktora_zmienila_definicje/10x-9be2887f1510a040249654b274bb71f5769fd191-im-33,33,33-FF,FF,FF.gif) to
to 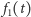 znajduje się w kwadracie
znajduje się w kwadracie 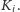
Aby skonstruować łamaną 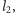 zastąpimy każdy z odcinków łamanej
zastąpimy każdy z odcinków łamanej 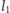 jej trzykrotnie pomniejszoną kopią, w taki sposób, by początek pomniejszonej łamanej pokrywał się z początkiem zastępowanego odcinka (Rys. 2). Następny wyraz naszego ciągu, funkcja
jej trzykrotnie pomniejszoną kopią, w taki sposób, by początek pomniejszonej łamanej pokrywał się z początkiem zastępowanego odcinka (Rys. 2). Następny wyraz naszego ciągu, funkcja ![| f2 [0,1] K,](/math/temat/matematyka/analiza/2013/06/28/Konstrukcja_ktora_zmienila_definicje/3x-946a1ad49cf8ed0cc64fe61c30511a93b64236f6-im-33,33,33-FF,FF,FF.gif) opisuje położenie punktu poruszającego się po krzywej
opisuje położenie punktu poruszającego się po krzywej 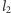 z prędkością
z prędkością 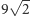 zgodnie z kierunkiem wskazanym przez strzałki na rysunku 2. Przyjmijmy, że wraz z łamaną
zgodnie z kierunkiem wskazanym przez strzałki na rysunku 2. Przyjmijmy, że wraz z łamaną 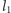 takim samym operacjom (pomniejszenia i odpowiedniego wklejania) podlega cały rysunek 1. Otrzymujemy w ten sposób rodzinę 81 kwadratów o boku
takim samym operacjom (pomniejszenia i odpowiedniego wklejania) podlega cały rysunek 1. Otrzymujemy w ten sposób rodzinę 81 kwadratów o boku 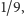 przy czym każdemu z nich przypisana jest pewna liczba
przy czym każdemu z nich przypisana jest pewna liczba 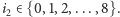 Każdemu z kwadratów nadajemy unikalny "numer katalogowy" złożony z dwóch liczb umożliwiających jego odnalezienie: pierwsza liczba jest równa
Każdemu z kwadratów nadajemy unikalny "numer katalogowy" złożony z dwóch liczb umożliwiających jego odnalezienie: pierwsza liczba jest równa 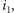 jeśli kwadrat znajduje się w kwadracie
jeśli kwadrat znajduje się w kwadracie 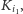 zaś druga,
zaś druga, 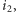 to wspomniana wcześniej liczba przypisana kwadratowi w wyniku konstrukcji. Kwadrat o numerze
to wspomniana wcześniej liczba przypisana kwadratowi w wyniku konstrukcji. Kwadrat o numerze 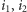 będziemy oznaczać przez
będziemy oznaczać przez 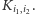 Podobnie jak w pierwszym kroku, obserwujemy, że jeśli
Podobnie jak w pierwszym kroku, obserwujemy, że jeśli ![i i i i+1 t∈ [19-+ 292, 19 +-292 ],](/math/temat/matematyka/analiza/2013/06/28/Konstrukcja_ktora_zmienila_definicje/14x-946a1ad49cf8ed0cc64fe61c30511a93b64236f6-im-33,33,33-FF,FF,FF.gif) to
to 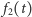 zawarte jest w kwadracie
zawarte jest w kwadracie 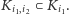
Kolejne łamane i funkcje generujemy, powtarzając powyższe operacje. Łamana 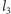 powstaje w wyniku trzykrotnego pomniejszenia łamanej
powstaje w wyniku trzykrotnego pomniejszenia łamanej 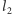 i zastąpienia nią w opisany uprzednio sposób wszystkich odcinków wyjściowej krzywej
i zastąpienia nią w opisany uprzednio sposób wszystkich odcinków wyjściowej krzywej 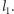
Dla dowolnego 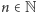 funkcja
funkcja ![fn [0,1] K](/math/temat/matematyka/analiza/2013/06/28/Konstrukcja_ktora_zmienila_definicje/2x-4faf81b3db9119ac5b2b130b4454fb21434ddde9-im-33,33,33-FF,FF,FF.gif) opisuje położenie punktu poruszającego się z prędkością
opisuje położenie punktu poruszającego się z prędkością 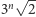 po łamanej
po łamanej 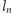 powstałej przez zastąpienie odcinków łamanej
powstałej przez zastąpienie odcinków łamanej 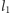 trzykrotnie pomniejszonymi kopiami łamanej
trzykrotnie pomniejszonymi kopiami łamanej 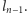
W każdym kroku konstrukcji otrzymujemy również rodzinę coraz drobniejszych kwadratów, którym przypisujemy odpowiednie numery katalogowe. W 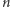 -tym kroku konstrukcji dostajemy
-tym kroku konstrukcji dostajemy 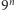 kwadratów o boku
kwadratów o boku 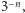 których numer katalogowy składa się z
których numer katalogowy składa się z  cyfr ze zbioru
cyfr ze zbioru 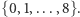 Kwadrat o numerze
Kwadrat o numerze 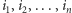 łatwo odnaleźć - wybieramy kwadrat pierwszego podziału o numerze
łatwo odnaleźć - wybieramy kwadrat pierwszego podziału o numerze 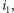 wewnątrz którego znajdujemy kwadrat drugiego podziału z numerem
wewnątrz którego znajdujemy kwadrat drugiego podziału z numerem 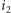 i tak dalej - z każdym kolejnym indeksem zawężając obszar poszukiwań, by w
i tak dalej - z każdym kolejnym indeksem zawężając obszar poszukiwań, by w 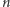 -tym kroku dotrzeć do odpowiedniego kwadratu
-tym kroku dotrzeć do odpowiedniego kwadratu  -tego podziału.
-tego podziału.
Warto zauważyć, że
![i1 i2 in i1 i2 in + 1 jeśli t ∈[--+ -2 + ...+-n,-- + -2 + ...+--n--], to fn(t) ∈ Ki1,i2,...,in, 9 9 9 9 9 9](/math/temat/matematyka/analiza/2013/06/28/Konstrukcja_ktora_zmienila_definicje/1x-9d0d5e0b7cf4d6424601b0807481f3db3cd1f76b-dm-33,33,33-FF,FF,FF.gif)
skąd można wywnioskować, że 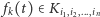 dla wszystkich
dla wszystkich 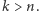
Wykażemy, że tak skonstruowany ciąg funkcyjny jest zbieżny, funkcja 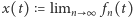 ciągła, a każdy punkt kwadratu jest postaci
ciągła, a każdy punkt kwadratu jest postaci 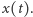 Zacznijmy od dowodu tej ostatniej własności. Zauważmy, że każdy
Zacznijmy od dowodu tej ostatniej własności. Zauważmy, że każdy 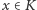 możemy opisać (niejednoznacznie) jako przecięcie pewnej nieskończonej rodziny kwadratów powstałych w kolejnych krokach konstrukcji. Zatem każdemu punktowi
możemy opisać (niejednoznacznie) jako przecięcie pewnej nieskończonej rodziny kwadratów powstałych w kolejnych krokach konstrukcji. Zatem każdemu punktowi 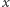 możemy przypisać nieskończony numer katalogowy
możemy przypisać nieskończony numer katalogowy 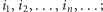 wówczas
wówczas 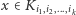 dla każdego
dla każdego 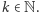 Niech
Niech

co oznacza, że następujące po przecinku cyfry rozwinięcia 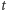 w systemie dziewiątkowym to
w systemie dziewiątkowym to 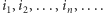 Pokażemy, że
Pokażemy, że 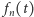 zbiega do punktu
zbiega do punktu 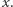 Ponieważ
Ponieważ ![| i1 i1+1 t ∈[ 9, 9 ],](/math/temat/matematyka/analiza/2013/06/28/Konstrukcja_ktora_zmienila_definicje/13x-3307253a98e73c210d2441444cd0037d12ca76c7-im-33,33,33-FF,FF,FF.gif) to dla
to dla 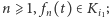 analogicznie, ponieważ
analogicznie, ponieważ ![i i i i+1 |t∈ [19 + 922,91+ 292-],](/math/temat/matematyka/analiza/2013/06/28/Konstrukcja_ktora_zmienila_definicje/15x-3307253a98e73c210d2441444cd0037d12ca76c7-im-33,33,33-FF,FF,FF.gif) to dla
to dla 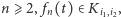 i ogólnie, jeśli
i ogólnie, jeśli 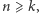 to
to 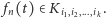 Zatem dla dowolnego
Zatem dla dowolnego 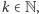 dla
dla 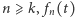 i
i  należą do tego samego kwadratu
należą do tego samego kwadratu 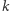 -tego podziału, czyli ich odległość
-tego podziału, czyli ich odległość 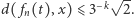 To dowodzi żądanej zbieżności.
To dowodzi żądanej zbieżności.
Powyższe rozumowanie dowodzi zbieżności ciągu 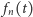 tylko dla wybranych
tylko dla wybranych 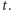 Aby wykazać ją dla wszystkich
Aby wykazać ją dla wszystkich ![t∈ [0,1],](/math/temat/matematyka/analiza/2013/06/28/Konstrukcja_ktora_zmienila_definicje/3x-717d359b6c0033087e9eaccf81f681ad4eea2f67-im-33,33,33-FF,FF,FF.gif) wystarczy zauważyć, że każdą liczbę można wyrazić w systemie dziewiątkowym, zatem każdemu
wystarczy zauważyć, że każdą liczbę można wyrazić w systemie dziewiątkowym, zatem każdemu ![|t∈ [0,1]](/math/temat/matematyka/analiza/2013/06/28/Konstrukcja_ktora_zmienila_definicje/4x-717d359b6c0033087e9eaccf81f681ad4eea2f67-im-33,33,33-FF,FF,FF.gif) możemy przypisać punkt
możemy przypisać punkt 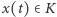 o nieskończonym indeksie odpowiadającym rozwinięciu dziewiątkowemu
o nieskończonym indeksie odpowiadającym rozwinięciu dziewiątkowemu 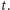 Powtarzając poprzednie rozumowanie, stwierdzamy, że
Powtarzając poprzednie rozumowanie, stwierdzamy, że 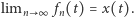 Pozostaje wykazać ciągłość funkcji
Pozostaje wykazać ciągłość funkcji 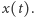
Zauważmy, że dzięki ciągłości każdej z funkcji 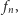 dla
dla 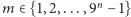 obraz przedziału
obraz przedziału ![[m9−1n , m9+n1]](/math/temat/matematyka/analiza/2013/06/28/Konstrukcja_ktora_zmienila_definicje/3x-c04b123cf5a580994e8410fc9f9409d0a1b5febc-im-33,33,33-FF,FF,FF.gif) należy do dwóch sąsiadujących kwadratów
należy do dwóch sąsiadujących kwadratów 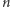 -tego podziału. Z wcześniejszych obserwacji wynika, że jeśli
-tego podziału. Z wcześniejszych obserwacji wynika, że jeśli 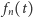 należy do pewnego kwadratu
należy do pewnego kwadratu  -tego podziału, to
-tego podziału, to 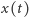 również. Weźmy teraz dowolny ciąg
również. Weźmy teraz dowolny ciąg 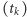 zbieżny do
zbieżny do 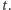 Jeśli
Jeśli 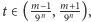 to począwszy od pewnego
to począwszy od pewnego 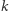 - oznaczmy je przez
- oznaczmy je przez 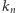 - wszystkie wyrazy ciągu
- wszystkie wyrazy ciągu 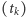 również należą do tego przedziału, zatem dla
również należą do tego przedziału, zatem dla 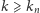 wszystkie wyrazy ciągu
wszystkie wyrazy ciągu 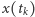 należą do dwóch sąsiadujących kwadratów
należą do dwóch sąsiadujących kwadratów  -tego podziału, przy czym do jednego z nich należy również
-tego podziału, przy czym do jednego z nich należy również 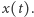 Oznacza to, że dla
Oznacza to, że dla 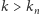 odległość
odległość 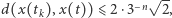 zatem
zatem 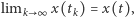 czyli funkcja
czyli funkcja ![x [0,1] K](/math/temat/matematyka/analiza/2013/06/28/Konstrukcja_ktora_zmienila_definicje/21x-c04b123cf5a580994e8410fc9f9409d0a1b5febc-im-33,33,33-FF,FF,FF.gif) jest ciągła.
jest ciągła.
Istnienie krzywych wypełniających kwadrat spowodowało konieczność poszukiwania przez matematyków innych definicji krzywych, lepiej oddających intuicje. Jedną z dróg prowadzących do celu jest zabezpieczenie się przed zgubnymi efektami działania nieskończoności - można zastrzec, by krzywa miała skończoną długość, żądając, by funkcja z pierwotnej definicji była nie tylko ciągła, ale by nie pozwoliła na zbyt szybkie rozciąganie odcinka ![|[0, 1],](/math/temat/matematyka/analiza/2013/06/28/Konstrukcja_ktora_zmienila_definicje/1x-2692ef288c615179aae0d1e0e3d13bdb2fa0d50e-im-33,33,33-FF,FF,FF.gif) czyli była np. funkcją o ciągłej pochodnej.
czyli była np. funkcją o ciągłej pochodnej.
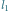 i kwadraty pierwszego podziału; poniżej krzywa odwiedzająca kwadraty w tej samej kolejności co
i kwadraty pierwszego podziału; poniżej krzywa odwiedzająca kwadraty w tej samej kolejności co 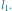
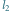 i kwadraty drugiego podziału.
i kwadraty drugiego podziału.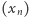 jest zbieżny do
jest zbieżny do 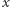 wtedy i tylko wtedy, gdy ciąg ich odległości od
wtedy i tylko wtedy, gdy ciąg ich odległości od 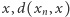 jest zbieżny do zera.
jest zbieżny do zera.