Lew i człowiek
Około 1930 roku Richard Rado (1906-1989) postawił następujący problem: Lew
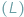 i człowiek
i człowiek
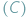 – traktowani jako punkty – poruszają się
w domkniętym kole jednostkowym z jednakowymi maksymalnymi
prędkościami. Czy (głodny) lew zawsze złapie człowieka?
– traktowani jako punkty – poruszają się
w domkniętym kole jednostkowym z jednakowymi maksymalnymi
prędkościami. Czy (głodny) lew zawsze złapie człowieka?
Przez ponad dwadzieścia lat wierzono, że w tej „grze” lew jest zawsze zwycięzcą. Uzasadniała to następująca strategia:
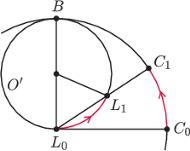
Rys. 1
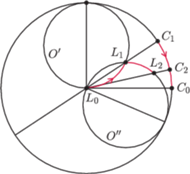
Rys. 2

Rys. 3
Rys. 4
Strategia lwa. Lew, przechodząc do środka koła, zmusza człowieka do zajęcia
pozycji na brzegu koła i ucieczki z maksymalną prędkością wzdłuż brzegu
koła (każde odejście człowieka od brzegu to zbliżenie się do lwa). Załóżmy,
że lew znajduje się początkowo w punkcie
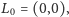 a człowiek
w punkcie
a człowiek
w punkcie
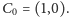 Sprytny lew przemieszcza się z maksymalną
prędkością, stale pozostając na promieniu
Sprytny lew przemieszcza się z maksymalną
prędkością, stale pozostając na promieniu
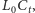 gdzie
gdzie
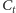 jest
położeniem człowieka w chwili
jest
położeniem człowieka w chwili
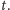 Oznacza to, że lew biegnie po łuku
mniejszego okręgu
Oznacza to, że lew biegnie po łuku
mniejszego okręgu
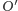 (o promieniu
(o promieniu
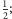 rysunek 1). Ponieważ łuki
rysunek 1). Ponieważ łuki
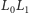 i
i
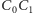 są równej długości (lew i człowiek biegną
z jednakowymi maksymalnymi prędkościami), więc lew spotka człowieka
w punkcie
są równej długości (lew i człowiek biegną
z jednakowymi maksymalnymi prędkościami), więc lew spotka człowieka
w punkcie
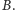 Nagła zmiana kierunku ucieczki człowieka, np.
w punkcie
Nagła zmiana kierunku ucieczki człowieka, np.
w punkcie
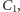 nie poprawia sytuacji człowieka! Lew, odbijając
symetrycznie mały okrąg
nie poprawia sytuacji człowieka! Lew, odbijając
symetrycznie mały okrąg
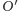 wzdłuż prostej
wzdłuż prostej
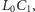 będzie biegł po
łuku
będzie biegł po
łuku
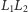 okręgu
okręgu
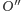 (rysunek 2). Zatem, bez względu
na
(rysunek 2). Zatem, bez względu
na
tor ucieczki człowieka po brzegu koła, zostanie on złapany i to w czasie nie większym niż czas potrzebny na to, by lew przebiegł połowę obwodu mniejszego okręgu.
Uwaga. Przypadek ten pokazuje, że często spotykana sugestia „najlepszą metodą pościgu jest pościg w kierunku uciekającego” w wielu sytuacjach nie ma żadnego racjonalnego uzasadnienia – gdyby w rozpatrywanej „grze” lew biegł w kierunku uciekającego człowieka – wzdłuż tzw. krzywej pościgu – to pozostałby głodny (rysunek 3).
Dopiero w 1952 r. – ponad dwadzieścia lat po postawieniu problemu – Abram S. Besicovitch (1891-1970) zauważył, że nieuzasadnione jest zakładanie, iż najlepszą strategią dla człowieka jest „być jak najdalej od lwa i poruszać się wzdłuż brzegu koła”, oraz zaproponował błyskotliwy sposób skutecznej ucieczki przed lwem. Opisał to J.E. Littlewood w A Mathematician’s Miscellany, Methuen and Co., Ltd., London 1953, s. 135-136.
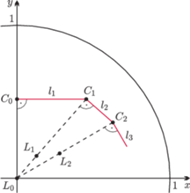
Strategia człowieka (Besicovitch). Załóżmy, że lew znajduje się
w punkcie
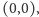 a człowiek w punkcie
a człowiek w punkcie
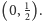 Kolejne
pozycje zajmowane przez lwa i człowieka – zawsze poruszających się
z jednakowymi maksymalnymi prędkościami – będziemy oznaczać literami
Kolejne
pozycje zajmowane przez lwa i człowieka – zawsze poruszających się
z jednakowymi maksymalnymi prędkościami – będziemy oznaczać literami
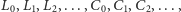 odpowiednio. Człowiek przemieszcza się
wzdłuż łamanej o wierzchołkach
odpowiednio. Człowiek przemieszcza się
wzdłuż łamanej o wierzchołkach
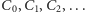 utworzonej z odcinków
o długościach
utworzonej z odcinków
o długościach

gdzie każdy odcinek
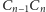 jest prostopadły do promienia
jest prostopadły do promienia
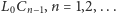 (rysunek 4).
(rysunek 4).
Wówczas:
Po pierwsze, całkowita długość łamanej
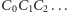 jest nieskończona,
bo
jest nieskończona,
bo

(gdyby było
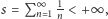 to wobec
to wobec

mielibyśmy sprzeczność).
Po drugie, lew nie może złapać człowieka.
Istotnie. Niech człowiek przemieszcza się po odcinku, a lew utrzymuje się na
promieniu
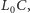 jak zostało to ustalone w Strategii lwa. Ponieważ
odcinek
jak zostało to ustalone w Strategii lwa. Ponieważ
odcinek
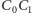 jest prostopadły do promienia
jest prostopadły do promienia
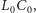 więc
lew nie może złapać człowieka, gdy człowiek przebiega odcinek
więc
lew nie może złapać człowieka, gdy człowiek przebiega odcinek
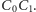 Podobnie, ponieważ odcinek
Podobnie, ponieważ odcinek
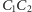 jest prostopadły do
promienia
jest prostopadły do
promienia
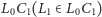 , więc lew nie może złapać człowieka, gdy
człowiek przebiega odcinek
, więc lew nie może złapać człowieka, gdy
człowiek przebiega odcinek
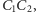 i tak we wszystkich pozostałych
odcinkach nieskończenie długiej łamanej.
i tak we wszystkich pozostałych
odcinkach nieskończenie długiej łamanej.
Uwaga. Łamana
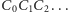 nie musi tworzyć „spirali”, biegnąc np. stale
zgodnie z ruchem wskazówek zegara, ale w każdym z wierzchołków może
zmienić kierunek na przeciwny. Gdy zaś lew porusza się według innych zasad,
to należy spojrzeć, gdzie lew znajduje się w
nie musi tworzyć „spirali”, biegnąc np. stale
zgodnie z ruchem wskazówek zegara, ale w każdym z wierzchołków może
zmienić kierunek na przeciwny. Gdy zaś lew porusza się według innych zasad,
to należy spojrzeć, gdzie lew znajduje się w
 -tym kroku – jeśli
-tym kroku – jeśli
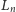 znajduje się we wnętrzu jednej z półpłaszczyzn wyznaczonych przez
prostą
znajduje się we wnętrzu jednej z półpłaszczyzn wyznaczonych przez
prostą
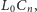 to człowiek powinien przemieszczać się (wzdłuż łamanej)
w kierunku półpłaszczyzny bez lwa.
to człowiek powinien przemieszczać się (wzdłuż łamanej)
w kierunku półpłaszczyzny bez lwa.
Co więcej, łamana
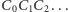 zawiera się we wnętrzu koła jednostkowego.
zawiera się we wnętrzu koła jednostkowego.
Z twierdzenia Pitagorasa bowiem mamy (rysunek 4):

więc

a stąd dla
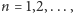 zachodzi
zachodzi
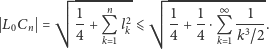 | (1) |
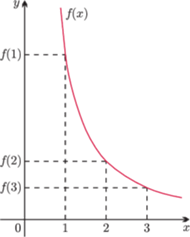
Rys. 5
Aby oszacować (od góry) wartość wyrażenia
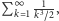 rozważmy
funkcję
rozważmy
funkcję
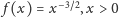 (rysunek 5). Wówczas
(rysunek 5). Wówczas

Ponieważ

więc
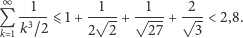 | (2) |
Stosując oszacowanie
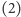 w wyrażeniu
w wyrażeniu
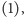 otrzymujemy
otrzymujemy

co kończy uzasadnienie poprawności strategii Besicovitcha.
Istnieje wiele wariantów problemu Rado, na przykład:
Szpaki i mucha. W
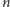 -wymiarowej kuli jednostkowej znajdują się szpaki
i jedna mucha. Wszyscy poruszają się z jednakową maksymalną prędkością.
Jaka minimalna liczba szpaków gwarantuje pochwycenie muchy? (Odpowiedź:
-wymiarowej kuli jednostkowej znajdują się szpaki
i jedna mucha. Wszyscy poruszają się z jednakową maksymalną prędkością.
Jaka minimalna liczba szpaków gwarantuje pochwycenie muchy? (Odpowiedź:
 szpaków wystarczy, a
szpaków wystarczy, a
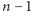 nie.)
nie.)
Niektóre z tego typu problemów wciąż czekają na swoich pogromców. Jeden z nich ma wyjątkowo proste sformułowanie.
Lwy na polu golfowym. Czy dwa lwy złapią człowieka na ograniczonym polu golfowym ze skończenie wieloma jeziorkami? (Zakładamy, że wszyscy uczestnicy „gry” poruszają się z jednakowymi maksymalnymi prędkościami, nie mogą wchodzić do wody, a brzegi jeziorek są krzywymi gładkimi.)