W Delcie nr 9 z 2012 r. pojawiło się zadanie:

Chciałbym dodać uzasadnienie geometryczne, czy też wyjaśnić jej znaczenie geometryczne.

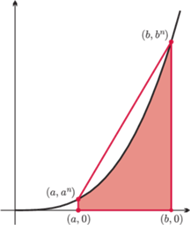
Rys. 1

Przepiszmy nierówność w postaci

Bez straty ogólności rozważań można przyjąć, że  Otóż prawa strona to pole trapezu o podstawach  i wysokości  Lewa to (zacienione) pole pod wykresem funkcji 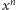 ograniczonej do przedziału 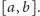 Ponieważ funkcja 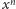 jest ściśle wypukła na półprostej 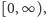 więc jej wykres znajduje się pod dowolną cięciwą. Oznacza to, że obszar pod wykresem jest zawarty w trapezie o wierzchołkach 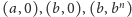 i 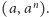  No i czego tu dowodzić?

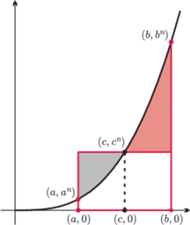
Rys. 2

Po rozwiązaniu podanym w miesięczniku jest uwaga o nierówności

równoważnej

Niech 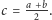 Tym razem pole pod wykresem funkcji 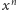 ma okazać się większe od pola prostokąta o podstawie  i wysokości 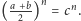 Wynika to z tego, że jeśli 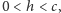 to

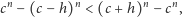(W)

co jest równoważne nierówności

więc wynikającej natychmiast ze ścisłej wypukłości funkcji 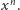 Z nierówności (W) wynika od razu, że symetria względem punktu 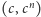 przekształca obszar szary na zbiór zawarty, ale niewypełniający obszaru kolorowego, więc nierówność jest prawdziwa.

Wypukłość funkcji 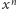 na półprostej 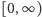 można wywnioskować z tego, że jej pochodna, czyli 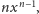 jest ściśle rosnąca na 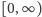 lub – jeśli ktoś nie lubi pochodnych – z ciągłości funkcji 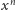 i nierówności

prawdziwej dla różnych liczb dodatnich 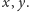 Można jej dowieść indukcyjnie. Krok indukcyjny polega na pomnożeniu obu stron nierówności

przez liczbę dodatnią

i stwierdzeniu, że

czyli

Ostatnia nierówność jest równoważna takiej 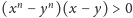 prawdziwej w oczywisty sposób.