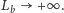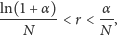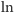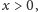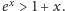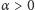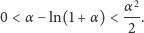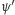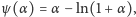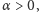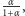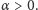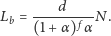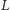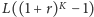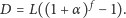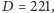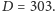Jak to działa?
O podatku Belki
Osoby osiągające dochody muszą płacić podatki. Podatki od pensji są najczęściej obliczane i odprowadzane przez instytucje, w których pracujemy. Podatki od dochodów uzyskiwanych na kontach bankowych są odprowadzane, w wysokości 19%, przez banki. Jest to tak zwany podatek Belki.
Przy obliczaniu tego podatku dwukrotnie dokonuje się zaokrąglenia: przy
obliczaniu dochodu (podstawy opodatkowania) i przy obliczaniu samego
podatku. Bankowcy zauważyli, że jeżeli dochód nie przekracza kwoty
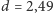 zł, to kwota podatku jest równa
zł, to kwota podatku jest równa
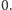 Mianowicie, kwota
Mianowicie, kwota
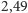 po pierwszym zaokrągleniu zamienia się na 2, a
po pierwszym zaokrągleniu zamienia się na 2, a
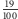 tej kwoty
to
tej kwoty
to
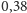 i drugie zaokrąglenie daje
i drugie zaokrąglenie daje
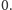 W związku z tym
niektóre banki zaproponowały lokaty na
W związku z tym
niektóre banki zaproponowały lokaty na
 dni z oprocentowaniem
dni z oprocentowaniem
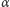 w skali rocznej, dla których dochody są naliczane każdego dnia.
Powstaje więc pytanie:
w skali rocznej, dla których dochody są naliczane każdego dnia.
Powstaje więc pytanie:
Jaka jest maksymalna kwota
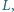 którą można ulokować na koncie, by
bank nie odprowadził od niej żadnego podatku?
którą można ulokować na koncie, by
bank nie odprowadził od niej żadnego podatku?
Dochody każdego dnia są obliczane zgodnie z procentem składanym
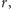 spełniającym równanie
spełniającym równanie

gdzie
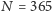 to liczba dni w roku. Maksymalna lokata
to liczba dni w roku. Maksymalna lokata
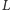 dana
jest równaniem
dana
jest równaniem
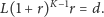 | (1) |
Przedostatniego dnia kwota do opodatkowania wynosi
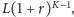 a dochód
od niej jest równy
a dochód
od niej jest równy
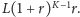 Stąd wzór.
Stąd wzór.
Do uzyskania konkretnych informacji, jakie kwoty wchodzą tu w grę i jak duży może być nieopodatkowany dochód, proponujemy rozwiązanie kilku zadań.
Aby oszacować błąd, który powstaje w obliczeniach przy zamianie
 na
na
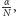 warto rozwiązać
warto rozwiązać
Na przykład, gdy
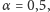 to błąd popełniany przy zamianie liczby
to błąd popełniany przy zamianie liczby
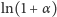 na liczbę
na liczbę
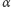 jest mniejszy niż
jest mniejszy niż
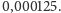 Zamieniając
w równaniu (1)
Zamieniając
w równaniu (1)
 na
na
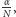 otrzymujemy, że od lokat
w wysokości
otrzymujemy, że od lokat
w wysokości
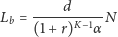 | (2) |
nie będzie się płacić podatku. Jest to lokata „bezpieczna”, nieznacznie
różniąca się od lokaty maksymalnej. Wzór (2) łatwo wykorzystać do
obliczeń. Banki proponują 3- lub 4-miesięczne lokaty unikające podatku Belki
i wygodnie jest wprowadzić do wzoru (3) liczbę
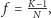 mierzącą
część roku, na którą lokata jest zakładana. Możemy wtedy wyeliminować
mierzącą
część roku, na którą lokata jest zakładana. Możemy wtedy wyeliminować
 ze wzoru (2).
ze wzoru (2).
- 1)
-
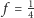 (lokata na 3 miesiące) przy oprocentowaniu
(lokata na 3 miesiące) przy oprocentowaniu
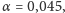 to (w przybliżeniu)
to (w przybliżeniu)
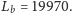
- 2)
-
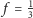 (lokata na 4 miesiące) i
(lokata na 4 miesiące) i
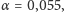 to
(w przybliżeniu)
to
(w przybliżeniu)
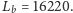
Gdyby podatek od dochodu odprowadzała osoba wykupująca lokatę,
to po okresie odpowiednio
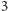 lub
lub
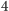 miesięcy musiałaby
odprowadzić odpowiednio 42 lub 58 złotych. Ponieważ w trakcie
trwania lokaty nie mogłaby ona pobrać zgromadzonych środków, więc,
z jej perspektywy, wzbogaca się ona dopiero po 3 lub, odpowiednio, po
4 miesiącach. Zabieg omijania podatku Belki rodzi więc istotne problemy prawne
i moralne i nie wszystkie banki zdecydowały się, by antybelkowe lokaty
oferować. Omijanie podatku trwa już kilka lat. Zaokrąglanie kwot do
pełnych złotówek w górę lub zaniechanie zaokrągleń zlikwidowałoby tę
możliwość.
miesięcy musiałaby
odprowadzić odpowiednio 42 lub 58 złotych. Ponieważ w trakcie
trwania lokaty nie mogłaby ona pobrać zgromadzonych środków, więc,
z jej perspektywy, wzbogaca się ona dopiero po 3 lub, odpowiednio, po
4 miesiącach. Zabieg omijania podatku Belki rodzi więc istotne problemy prawne
i moralne i nie wszystkie banki zdecydowały się, by antybelkowe lokaty
oferować. Omijanie podatku trwa już kilka lat. Zaokrąglanie kwot do
pełnych złotówek w górę lub zaniechanie zaokrągleń zlikwidowałoby tę
możliwość.
Na zakończenie zauważamy, że gdyby bank naliczał odsetki nie każdego
dnia, ale co godzinę, to we wzorze (3) liczbę
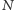 należałoby zamienić na
należałoby zamienić na
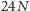 i „bezpieczna” wysokość lokaty wzrosłaby 24-krotnie, podobnie
jak wysokość nieopodatkowanego dochodu.
i „bezpieczna” wysokość lokaty wzrosłaby 24-krotnie, podobnie
jak wysokość nieopodatkowanego dochodu.
Gdy
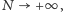 to i
to i