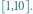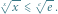O wieżach potęgowych (II)
Spróbujmy rozwiązać następujące zadanie:
Zadanie. Znaleźć takie 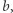 dla którego
dla którego
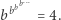 |
Zauważmy, że wykładnik 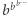 liczby
liczby 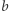 w równaniu jest równy całemu wyrażeniu (które jest równe 4). Wynika z tego równość
w równaniu jest równy całemu wyrażeniu (które jest równe 4). Wynika z tego równość 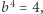 a więc
a więc 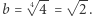 Gotowe. Czytelników Zaniepokojonych tak prostym rozwiązaniem prosimy o cierpliwość. Teraz drugie zadanie: rozwiązać równanie
Gotowe. Czytelników Zaniepokojonych tak prostym rozwiązaniem prosimy o cierpliwość. Teraz drugie zadanie: rozwiązać równanie
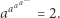 |
Postępując podobnie jak wyżej, otrzymujemy 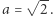 Ale w takim razie
Ale w takim razie 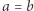 oraz
oraz
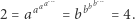 |
Zachęcamy Czytelnika do próby wyjaśnienia tego paradoksu przed lekturą kolejnych akapitów.
W artykule Porównywanie wież potęgowych (Delta 2/2019) wprowadziliśmy następującą notację:
![a::: [a ,a ,a ,...] = aa23, 1 2 3 1](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/1x-63a0f6089e28d7a241d92de772ad48acf49e57f1-dm-33,33,33-FF,FF,FF.gif) |
gdzie 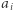 dla
dla 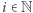 to dowolna dodatnia liczba rzeczywista. Jak należy rozumieć nieskończone wieże potęgowe? Formalnie jest to granica ciągu liczbowego
to dowolna dodatnia liczba rzeczywista. Jak należy rozumieć nieskończone wieże potęgowe? Formalnie jest to granica ciągu liczbowego
![[a1,a2,...] =nl im+∞[a1,a2,...,an].](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/4x-63a0f6089e28d7a241d92de772ad48acf49e57f1-dm-33,33,33-FF,FF,FF.gif) |
Zatem albo wieża definiuje pewną liczbę, albo jest rozbieżna. Dla uproszczenia notacji, jeżeli 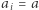 dla
dla  to będziemy zapisywać
to będziemy zapisywać ![|[a, a,...] = [a × ∞ ].](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/7x-63a0f6089e28d7a241d92de772ad48acf49e57f1-im-33,33,33-FF,FF,FF.gif) Przykładem wieży rozbieżnej jest
Przykładem wieży rozbieżnej jest ![|[2 × ∞ ] = +∞ ,](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/8x-63a0f6089e28d7a241d92de772ad48acf49e57f1-im-33,33,33-FF,FF,FF.gif) natomiast
natomiast ![[1× ∞ ] = 1.](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/9x-63a0f6089e28d7a241d92de772ad48acf49e57f1-im-33,33,33-FF,FF,FF.gif) Czy w takim razie w ogóle ma sens rozważać
Czy w takim razie w ogóle ma sens rozważać 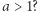
Które wieże zatem są zbieżne? W ogólnym przypadku, gdy składniki wieży są dowolne, trudno jest odpowiedzieć na to pytanie. My zajmiemy się prostszą sytuacją, gdy wieża ma postać ![[a × ∞ ].](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/1x-6761d3d114258ea9800218d229f58750b21bd579-im-33,33,33-FF,FF,FF.gif) Wtedy łatwo można wyznaczyć jej granicę. Istotnie, jeśli istnieje granica
Wtedy łatwo można wyznaczyć jej granicę. Istotnie, jeśli istnieje granica ![[a × ∞ ]](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/2x-6761d3d114258ea9800218d229f58750b21bd579-im-33,33,33-FF,FF,FF.gif) i wynosi ona
i wynosi ona 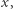 to zachodzi
to zachodzi
 |
To prowadzi do wniosku, że 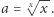 Ta równość wiąże w sposób istotny granicę wieży oraz jej składniki. W szczególności można ją traktować jak funkcję. Przyjrzyjmy się teraz następującemu twierdzeniu.
Ta równość wiąże w sposób istotny granicę wieży oraz jej składniki. W szczególności można ją traktować jak funkcję. Przyjrzyjmy się teraz następującemu twierdzeniu.
Twierdzenie (1). Niech  dla
dla 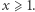 Wtedy:
Wtedy:
- 1.
![f [1,+∞ ) [1, e√ e];](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/8x-6761d3d114258ea9800218d229f58750b21bd579-im-33,33,33-FF,FF,FF.gif)
- 2.
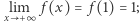
- 3.
- Jeśli
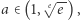 to równanie
to równanie  ma takie dwa rozwiązania
ma takie dwa rozwiązania 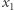 i
i 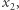 że
że  oraz
oraz 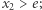
- 4.
- Jeśli
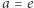 lub
lub 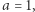 to równanie
to równanie  ma dokładnie jedno rozwiązanie;
ma dokładnie jedno rozwiązanie; - 5.
- Jeśli
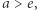 to równanie
to równanie 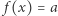 nie ma rozwiązań.
nie ma rozwiązań.
Z twierdzenia 1 możemy wyciągnąć wniosek, że jeśli 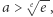 to
to ![|[a × ∞ ]](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/2x-d97d32a5c5adbaa1d504f83de461bb5ba9fcf4e4-im-33,33,33-FF,FF,FF.gif) nie istnieje. Dodatkowo, jeżeli
nie istnieje. Dodatkowo, jeżeli ![√e-- a ∈ [1, e ],](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/3x-d97d32a5c5adbaa1d504f83de461bb5ba9fcf4e4-im-33,33,33-FF,FF,FF.gif) to wtedy wieża
to wtedy wieża ![|[a × ∞ ]](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/4x-d97d32a5c5adbaa1d504f83de461bb5ba9fcf4e4-im-33,33,33-FF,FF,FF.gif) ma szansę być zbieżna. W szczególności, ponieważ
ma szansę być zbieżna. W szczególności, ponieważ  to
to ![√ -- [ ee × ∞ ] = e.](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/6x-d97d32a5c5adbaa1d504f83de461bb5ba9fcf4e4-im-33,33,33-FF,FF,FF.gif) Robert Arthur Knoebel dowodzi, że
Robert Arthur Knoebel dowodzi, że ![|[a × ∞ ]](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/7x-d97d32a5c5adbaa1d504f83de461bb5ba9fcf4e4-im-33,33,33-FF,FF,FF.gif) jest zbieżny wtedy i tylko wtedy, gdy
jest zbieżny wtedy i tylko wtedy, gdy ![|a∈ [e−e, e√ e].](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/8x-d97d32a5c5adbaa1d504f83de461bb5ba9fcf4e4-im-33,33,33-FF,FF,FF.gif) My zaś wykażemy zbieżność w przypadku
My zaś wykażemy zbieżność w przypadku 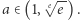
Twierdzenie (1'). Jeśli 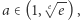 to
to ![[a ×∞ ]](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/2x-f3b2037efe781d857127042a301b74b5c27ddd15-im-33,33,33-FF,FF,FF.gif) jest dobrze określona.
jest dobrze określona.
Dowód. Wykażemy, że ciąg ![([a ×n])nA0](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/3x-f3b2037efe781d857127042a301b74b5c27ddd15-im-33,33,33-FF,FF,FF.gif) jest ciągiem rosnącym i ograniczonym, z tego będzie wynikała zbieżność.
jest ciągiem rosnącym i ograniczonym, z tego będzie wynikała zbieżność.
Najpierw wykażemy, że wartość wieży potęgowej ![|[a × n]](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/1x-06e436f246ac5cae8b68f795deb6d16d02973a72-im-33,33,33-FF,FF,FF.gif) jest mniejsza niż
jest mniejsza niż  dla każdego
dla każdego  Zauważmy, że
Zauważmy, że  Załóżmy teraz, że
Załóżmy teraz, że ![|[a × n] < e](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/5x-06e436f246ac5cae8b68f795deb6d16d02973a72-im-33,33,33-FF,FF,FF.gif) dla
dla 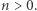 Wtedy
Wtedy
![-- [a × (n +1)] = [a,a × n] < [a, e] < [e√ e,e] = e.](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/7x-06e436f246ac5cae8b68f795deb6d16d02973a72-dm-33,33,33-FF,FF,FF.gif) |
Na mocy zasady indukcji matematycznej ciąg jest więc ograniczony. Teraz wykażemy, że jest rosnący. Po pierwsze zauważmy, że gdy 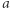 należy do rozważanego przedziału, to zachodzi nierówność
należy do rozważanego przedziału, to zachodzi nierówność 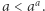 Załóżmy, że
Załóżmy, że ![[a × (n− 1)] > [a ×(n − 2)]](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/10x-06e436f246ac5cae8b68f795deb6d16d02973a72-im-33,33,33-FF,FF,FF.gif) i wywnioskujemy z tego, że
i wywnioskujemy z tego, że ![| [a ×n] > [a ×(n − 1)].](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/11x-06e436f246ac5cae8b68f795deb6d16d02973a72-im-33,33,33-FF,FF,FF.gif) Zachodzi
Zachodzi
![[a × n] = [a,a × (n −1)] > [a, a× (n − 2)] = [a× (n − 1)].](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/12x-06e436f246ac5cae8b68f795deb6d16d02973a72-dm-33,33,33-FF,FF,FF.gif) |
Z zasady indukcji mamy, że ciąg ![([a ×n]) nA0](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/13x-06e436f246ac5cae8b68f795deb6d16d02973a72-im-33,33,33-FF,FF,FF.gif) jest rosnący. Z faktu, że ciąg jest rosnący oraz ograniczony, wynika jego zbieżność.
jest rosnący. Z faktu, że ciąg jest rosnący oraz ograniczony, wynika jego zbieżność.
Powyższe rozważania możemy wykorzystać do sformułowania następujących równości:
![√ -- √4-- [ 2 × ∞ ] = [ 4 × ∞ ] = 2.](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/1x-8d205919cc2122189108b16c3e01e178ea78dc05-dm-33,33,33-FF,FF,FF.gif) |
Ciekawostką jest, że jeżeli  jest dodatnią liczbą naturalną, to tylko dla
jest dodatnią liczbą naturalną, to tylko dla 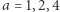 wartości wieże są liczbami wymiernymi - wszystkie pozostałe przypadki generują nie tylko liczby niewymierne, ale i przestępne! Ta i inne teorioliczbowe własności wież potęgowych zostały skumulowane w poniższym twierdzeniu.
wartości wieże są liczbami wymiernymi - wszystkie pozostałe przypadki generują nie tylko liczby niewymierne, ale i przestępne! Ta i inne teorioliczbowe własności wież potęgowych zostały skumulowane w poniższym twierdzeniu.
Twierdzenie (2). Niech 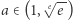 będzie liczbą algebraiczną. Wtedy:
będzie liczbą algebraiczną. Wtedy:
- 1.
- Jeśli
 dla wszystkich wymiernych
dla wszystkich wymiernych 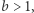 to
to ![[a × ∞ ]](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/4x-dcafc6bc9a7f5b84541c9ad303b5f464fbe432e1-im-33,33,33-FF,FF,FF.gif) jest liczbą przestępną;
jest liczbą przestępną; - 2.
- Jeśli
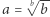 dla pewnej liczby wymiernej
dla pewnej liczby wymiernej 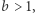 to:
to:
- (a)
- jeśli
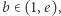 to
to ![|[a × ∞ ] = b,](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/8x-dcafc6bc9a7f5b84541c9ad303b5f464fbe432e1-im-33,33,33-FF,FF,FF.gif)
- (b)
- (przypadek przejściowy) jeśli
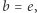 to
to ![[e√ e-×∞ ] = e](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/10x-dcafc6bc9a7f5b84541c9ad303b5f464fbe432e1-im-33,33,33-FF,FF,FF.gif) jest liczbą przestępną,
jest liczbą przestępną, - (c)
- jeśli
 to:
to:
- (i)
- jeśli
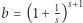 dla pewnej liczby całkowitej
dla pewnej liczby całkowitej 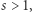 to
to ![s |[a × ∞ ] = (1+ 1s) ;](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/14x-dcafc6bc9a7f5b84541c9ad303b5f464fbe432e1-im-33,33,33-FF,FF,FF.gif) [Dla
[Dla  otrzymujemy
otrzymujemy  oraz
oraz 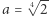 i
i  ],
], - (ii)
- jeśli
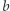 nie jest postaci
nie jest postaci  dla pewnej liczby całkowitej
dla pewnej liczby całkowitej  to
to ![[a ×∞ ]](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/22x-dcafc6bc9a7f5b84541c9ad303b5f464fbe432e1-im-33,33,33-FF,FF,FF.gif) jest liczbą przestępną.
jest liczbą przestępną.
Dowód Twierdzenia 2 można znaleźć w pracy: M. Vassilev-Missana, Some Results on Infinite Power Towers z 2010 roku.
Punkt 2(c)(i) powyższego twierdzenia można wykorzystać do rozwiązania w liczbach wymiernych równania
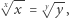 |
przy założeniach 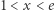 oraz
oraz  Wtedy
Wtedy
 |
W szczególności, dla  otrzymujemy
otrzymujemy 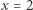 i
i 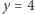 oraz równość
oraz równość 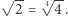 Dla
Dla 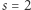 zaś otrzymujemy
zaś otrzymujemy 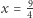 i
i 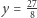 oraz równość
oraz równość 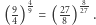 Czytelnik zechce samodzielnie sprawdzić słuszność powyższych równości.
Czytelnik zechce samodzielnie sprawdzić słuszność powyższych równości.
Wróćmy teraz do paradoksalnego rozumowania przedstawionego na początku artykułu. Przypomnijmy: wynika z niego, że 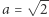 jest rozwiązaniem, ale samo rozumowanie prowadzące do tego wyniku nie jest satysfakcjonujące - dokonujemy pewnego podstawienia bez uprzedniej wiedzy na temat tego, czy
jest rozwiązaniem, ale samo rozumowanie prowadzące do tego wyniku nie jest satysfakcjonujące - dokonujemy pewnego podstawienia bez uprzedniej wiedzy na temat tego, czy ![|[a × ∞ ]](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/2x-7c418989495b558e0d83057ffacc3e0a9a7ad185-im-33,33,33-FF,FF,FF.gif) jest zbieżne. Dla
jest zbieżne. Dla 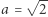 zdefiniujmy zatem
zdefiniujmy zatem ![a = [a× n]. n](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/4x-7c418989495b558e0d83057ffacc3e0a9a7ad185-im-33,33,33-FF,FF,FF.gif) Łatwo można wykazać zbieżność
Łatwo można wykazać zbieżność 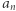 bez odwoływania się do trudnych twierdzeń. Mamy wszak
bez odwoływania się do trudnych twierdzeń. Mamy wszak 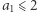 oraz
oraz
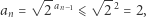 |
zatem na mocy zasady indukcji matematycznej 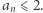 Ponadto oczywiście
Ponadto oczywiście 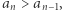 więc ciąg
więc ciąg 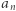 jest zbieżny. Niech
jest zbieżny. Niech 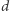 będzie jego granicą, wtedy
będzie jego granicą, wtedy 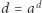 i skoro
i skoro 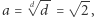 to
to 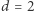 lub
lub  Jednak rozwiązanie
Jednak rozwiązanie  odrzucamy, gdyż
odrzucamy, gdyż 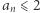 implikuje
implikuje 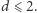 W takim razie
W takim razie ![√ -- |[ 2 × ∞ ] = 2,](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/19x-7c418989495b558e0d83057ffacc3e0a9a7ad185-im-33,33,33-FF,FF,FF.gif) ale zdecydowanie nie
ale zdecydowanie nie ![√ -- [ 44 × ∞ ] = 4.](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/20x-7c418989495b558e0d83057ffacc3e0a9a7ad185-im-33,33,33-FF,FF,FF.gif)
Dla jakich 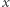 równanie
równanie
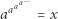 |
ma zatem rozwiązanie? Skoro ![[a× ∞ ]](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/3x-d94a0b8ebc991db2bea40563159ca49e6e961236-im-33,33,33-FF,FF,FF.gif) jest zbieżna (wtedy równanie ma sens) i
jest zbieżna (wtedy równanie ma sens) i ![a ∈ [e −e,√e e-]](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/4x-d94a0b8ebc991db2bea40563159ca49e6e961236-im-33,33,33-FF,FF,FF.gif) oraz funkcja
oraz funkcja
![-- g [e−e,√ee] ∋a ( [a × ∞ ]](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/5x-d94a0b8ebc991db2bea40563159ca49e6e961236-dm-33,33,33-FF,FF,FF.gif) |
jest rosnąca, to wystarczy obliczyć 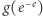 oraz
oraz 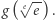 Ale to zadanie jest proste, gdyż jeśli
Ale to zadanie jest proste, gdyż jeśli ![|x = [a × ∞ ],](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/8x-d94a0b8ebc991db2bea40563159ca49e6e961236-im-33,33,33-FF,FF,FF.gif) to
to 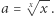 Zatem
Zatem
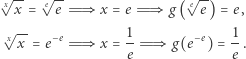
Tym samym ![|x ∈[e−1,e].](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/11x-d94a0b8ebc991db2bea40563159ca49e6e961236-im-33,33,33-FF,FF,FF.gif) W szczególności rozważane wcześniej równanie
W szczególności rozważane wcześniej równanie ![|[y× ∞ ] = 4](/math/temat/matematyka/analiza/2020/03/31/o-wiezach-potegowych/12x-d94a0b8ebc991db2bea40563159ca49e6e961236-im-33,33,33-FF,FF,FF.gif) nie ma rozwiązania.
nie ma rozwiązania.
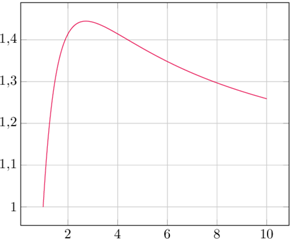
 dla
dla  w zakresie
w zakresie 
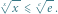
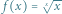 dla
dla  w zakresie
w zakresie