Proste zadanie o wielomianach
Weźmy wielomian 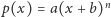 i obliczmy wszystkie jego niezerowe pochodne:
i obliczmy wszystkie jego niezerowe pochodne:

Widzimy, że 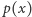 ma wspólny pierwiastek z każdą ze swoich pochodnych
ma wspólny pierwiastek z każdą ze swoich pochodnych 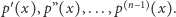 Czy są inne wielomiany o tej własności?
Czy są inne wielomiany o tej własności?
Zadanie 1. Niech 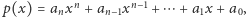 gdzie
gdzie 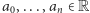 oraz
oraz 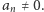 Przypuśćmy, że dla każdego
Przypuśćmy, że dla każdego 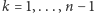 wielomiany
wielomiany 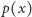 i
i 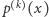 mają wspólny pierwiastek rzeczywisty. Udowodnij, że
mają wspólny pierwiastek rzeczywisty. Udowodnij, że 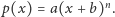
Wielomiany 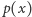 i
i 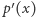 mają wspólny pierwiastek wtedy i tylko wtedy, gdy
mają wspólny pierwiastek wtedy i tylko wtedy, gdy 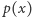 ma przynajmniej jeden pierwiastek wielokrotny. Tym samym rozwiązaliśmy zadanie dla
ma przynajmniej jeden pierwiastek wielokrotny. Tym samym rozwiązaliśmy zadanie dla 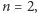 bo wielomian stopnia
bo wielomian stopnia 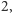 mający pierwiastek wielokrotny, jest postaci
mający pierwiastek wielokrotny, jest postaci 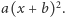 Dla
Dla 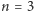 musimy jeszcze rozważyć wielomiany postaci
musimy jeszcze rozważyć wielomiany postaci 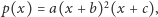 gdzie
gdzie 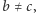 jednak taki wielomian nie może mieć wspólnego pierwiastka ze swoją drugą pochodną
jednak taki wielomian nie może mieć wspólnego pierwiastka ze swoją drugą pochodną 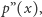 o czym przekonuje nas rzut oka na rysunek. Zatem także dla
o czym przekonuje nas rzut oka na rysunek. Zatem także dla 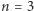 zadanie jest rozwiązane. Podobny argument - prosta analiza wzajemnego położenia pierwiastków wielomianu i jego pochodnych na podstawie twierdzenia Rolle'a - działa jeszcze dla
zadanie jest rozwiązane. Podobny argument - prosta analiza wzajemnego położenia pierwiastków wielomianu i jego pochodnych na podstawie twierdzenia Rolle'a - działa jeszcze dla 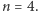
Spróbujmy inaczej. Dla dowolnych dwóch wielomianów 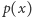 i
i 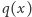 zdanie "
zdanie " 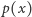 i
i 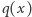 mają wspólny czynnik" można zapisać jako równanie algebraiczne zawierające współczynniki tych wielomianów. Czytelnikom zainteresowanym szczegółami polecamy zapoznanie się z pojęciem rugownika (ang. resultant) dwóch wielomianów. Wobec tego warunek z treści zadania prowadzi do układu
mają wspólny czynnik" można zapisać jako równanie algebraiczne zawierające współczynniki tych wielomianów. Czytelnikom zainteresowanym szczegółami polecamy zapoznanie się z pojęciem rugownika (ang. resultant) dwóch wielomianów. Wobec tego warunek z treści zadania prowadzi do układu 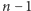 równań algebraicznych w zmiennych
równań algebraicznych w zmiennych 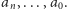 Na przykład dla
Na przykład dla 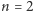 dostajemy znaną wszystkim "deltę":
dostajemy znaną wszystkim "deltę":

a dla 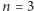 mamy warunki:
mamy warunki:

i tak dalej. Pozostaje wykazać, że jedyne rozwiązania tak otrzymanego układu odpowiadają współczynnikom wielomianów postaci 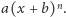 Jak dotychczas, możliwości obliczeniowe znanych algorytmów rozwiązywania układów równań algebraicznych kończą się na
Jak dotychczas, możliwości obliczeniowe znanych algorytmów rozwiązywania układów równań algebraicznych kończą się na 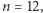 i w tym zakresie nasze zadanie można uznać za rozwiązane (zob. [1]).
i w tym zakresie nasze zadanie można uznać za rozwiązane (zob. [1]).
Jak ważne jest założenie, że 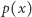 ma wspólny pierwiastek ze wszystkimi swoimi pochodnymi do rzędu
ma wspólny pierwiastek ze wszystkimi swoimi pochodnymi do rzędu 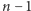 włącznie? Spójrzmy na przykład:
włącznie? Spójrzmy na przykład:

Wielomian 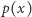 ma wspólny pierwiastek z każdą wymienioną pochodną z wyjątkiem pierwszej. Okazuje się, co więcej, że dla każdej takiej pary
ma wspólny pierwiastek z każdą wymienioną pochodną z wyjątkiem pierwszej. Okazuje się, co więcej, że dla każdej takiej pary 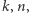 że
że 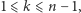 można skonstruować wielomian stopnia
można skonstruować wielomian stopnia 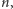 mający wspólny pierwiastek z każdą ze swoich pochodnych z wyjątkiem
mający wspólny pierwiastek z każdą ze swoich pochodnych z wyjątkiem 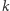 -tej, i który nie jest postaci
-tej, i który nie jest postaci 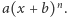 Czytelnik może się o tym przekonać, eksperymentując z jednym z wielu programów (np. [2] lub [4]) pozwalających wizualizować wzajemne położenie pierwiastków wielomianu i pierwiastków jego pochodnych. Ambitniejszy Czytelnik, wykorzystując twierdzenie Brouwera o punkcie stałym, może spróbować samodzielnie udowodnić nawet silniejsze twierdzenie: dla każdego wyboru
Czytelnik może się o tym przekonać, eksperymentując z jednym z wielu programów (np. [2] lub [4]) pozwalających wizualizować wzajemne położenie pierwiastków wielomianu i pierwiastków jego pochodnych. Ambitniejszy Czytelnik, wykorzystując twierdzenie Brouwera o punkcie stałym, może spróbować samodzielnie udowodnić nawet silniejsze twierdzenie: dla każdego wyboru 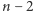 par liczb naturalnych
par liczb naturalnych 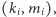 spełniających
spełniających 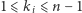 oraz
oraz 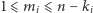 dla
dla 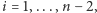 istnieje taki wielomian
istnieje taki wielomian 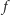 stopnia
stopnia 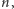 że
że 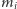 -ty co do wielkości pierwiastek
-ty co do wielkości pierwiastek 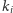 -tej pochodnej
-tej pochodnej 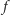 jest również pierwiastkiem
jest również pierwiastkiem 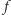 oraz
oraz 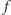 nie jest postaci
nie jest postaci 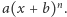
Czytelnik już na pewno podejrzewa, że nasze zadanie jest trudniejsze niż typowe zadanie olimpijskie, nawet jeżeli na takie wygląda. Faktycznie, jest ono znane jako hipoteza Casas-Alvero od nazwiska matematyka, który postawił ją na początku obecnego wieku w związku ze swoją pracą nad krzywymi algebraicznymi. Dokładniej rzecz biorąc, hipoteza Casas-Alvero mówi o wielomianach o współczynnikach zespolonych, mających wspólne pierwiastki zespolone ze swoimi pochodnymi. Nasze sformułowanie, potencjalnie łatwiejsze, jest jednak także problemem otwartym. Przez ponad dekadę nastąpił tylko nieznaczny postęp w pracach nad hipotezą, lecz Czytelnik nie powinien się tym zrażać - najprawdopodobniej niewielu matematyków nią się interesuje. Używając silnych narzędzi algebraicznych, udowodniono, na przykład, [3], że hipoteza jest prawdziwa dla wielomianów stopnia 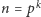 lub
lub 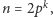 gdzie
gdzie 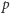 jest liczbą pierwszą i w kilku innych szczególnych przypadkach. Po bieżące wyniki odsyłamy do publikacji dostępnych w Internecie.
jest liczbą pierwszą i w kilku innych szczególnych przypadkach. Po bieżące wyniki odsyłamy do publikacji dostępnych w Internecie.