Gdzie tam znaczy też z powrotem
Każda ptaszyna swym własnym głosem Pana Boga chwali. Tym przysłowiem odpowiedziałem podczas obrony pracy doktorskiej na pytanie Profesora Andrzeja Mostowskiego, czemu zbudowałem aksjomatykę geometrii eliptycznej, podczas gdy można tę geometrię uprawiać analitycznie (czyli rachunkowo)...
A przypomniałem to sobie z okazji pytania, jakie przyszło mi do głowy właśnie na rachunkowym gruncie: jakie funkcje wymierne (poza tożsamością) są odwrotne same do siebie? Gdy przyszło, to ponieważ nie czuję się w środowisku algebraicznym u siebie, zadałem je Wybitnym Algebraikom. Wbrew moim oczekiwaniom odpowiedź nie wskazała tylko funkcji 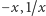 i
i 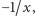 lecz dwie szerokie klasy
lecz dwie szerokie klasy

Natychmiast wobec tego zamieściłem w Delcie notkę, dzieląc się tą informacją z Czytelnikami (bo skoro ja nie wiedziałem, to zapewne nie wszyscy Czytelnicy o tym wiedzą) - jest w numerze 10/2010.
Ale pozostawało pytanie, dlaczego tak jest. Bo sprawdzenie, że to prawda, na pytanie dlaczego? nie odpowiada. I choć do dziś nie wiem, jak tę odpowiedź uzyskują algebraicy, gdy przetłumaczyłem problem na swój język, czyli geometrię, wszystko stało się zrozumiałe.
Przecież w geometrii funkcje odwrotne same do siebie (uczenie: inwolucje) to symetrie. Liczby zaś tworzą (już w podstawówce) prostą, zwaną osią, gdy nada się jej orientację. A symetrie na prostej to symetrie środkowe - jak łatwo zauważyć, symetria względem 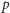 dana jest rachunkowym wzorem
dana jest rachunkowym wzorem 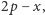 bo środek punktów
bo środek punktów 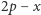 i
i 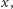 czyli ich średnia arytmetyczna, to
czyli ich średnia arytmetyczna, to 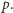 Mieści się to wśród przytoczonych funkcji
Mieści się to wśród przytoczonych funkcji 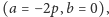 ale ich nie wyczerpuje.
ale ich nie wyczerpuje.
Wypada spojrzeć szerzej, czyli umieścić oś liczbową na płaszczyźnie. Na płaszczyźnie zachowują tę oś również symetrie względem prostopadłych do niej prostych - ale one nic nowego nie wnoszą: ograniczone do osi liczbowej są symetriami środkowymi. Są jednak i inne symetrie: inwersje (symetrie względem okręgów) i antyinwersje - jeśli środek okręgu umieścimy na osi liczbowej, również one dostarczą nam poszukiwanych inwolucji. Sprawdźmy.
Zgodnie z przypomnianą na marginesie definicją inwersja względem okręgu o środku 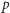 i promieniu
i promieniu 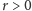 przekształca na osi punkt
przekształca na osi punkt  na taki punkt
na taki punkt 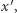 że
że

czyli

Zauważmy, że uzyskane tym sposobem funkcje prawie wyczerpują obie wymienione na początku klasy funkcji: podstawiając 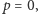 uzyskujemy wszystkie funkcje pierwszej z klas dla
uzyskujemy wszystkie funkcje pierwszej z klas dla 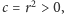 a dzieląc przez
a dzieląc przez 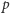 w pozostałych przypadkach - wszystkie funkcje drugiej z klas dla
w pozostałych przypadkach - wszystkie funkcje drugiej z klas dla 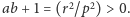 Pozostałe funkcje uzyskujemy z antyinwersji, bo dla niej
Pozostałe funkcje uzyskujemy z antyinwersji, bo dla niej

Wystarczyło, że przetłumaczyłem sobie algebrę na geometrię i wszystko stało się dla mnie jasne.
Ogólny morał z tego taki, że każdy problem, nie tylko matematyczny, należy sobie przetłumaczyć na język nam bliski, a wtedy wiele trudności zniknie.
Ba, mało: pojawi się wiele kwestii w mało używanej przez nas terminologii ukrywających się przed nami. W tym przypadku np. fakt, iż skoro jesteśmy na płaszczyźnie, to nie ma powodu, by ograniczać się do prostej - uzyskane wzory będą funkcjonowały dla wszystkich punktów płaszczyzny traktowanych jako liczby zespolone (algebraicy w swoim języku bez problemów widzą, że wzory te odpowiadają na pytanie, jak wyglądają wymierne inwolucje w dowolnym ciele). Możemy jednak pójść dalej: nasze wzory pracują w dowolnym (naturalnym) wymiarze, opisując nam geometrycznie inwolucje - czy znaczy to, że wzory te są poprawne również wśród kwaternionów, realizujących się jako punkty przestrzeni czterowymiarowej? A co znaczą dla innych wymiarów, w których punkty nie tworzą ciał?
I to jest drugi morał: z problemami jest jak z hydrą - gdy utniemy jej jedną głowę, w jej miejsce wyrasta kilka nowych.