Funkcja Lamberta
Określona na półprostej
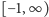 funkcja
funkcja
 jest ciągła
i rosnąca, a zbiorem jej wartości jest półprosta
jest ciągła
i rosnąca, a zbiorem jej wartości jest półprosta
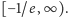 Można więc
jednoznacznie zdefiniować funkcję
Można więc
jednoznacznie zdefiniować funkcję
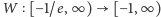 odwrotną
do
odwrotną
do
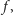 tj. taką, że
tj. taką, że
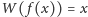 dla każdego
dla każdego
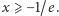
Funkcję tę nazywa się obecnie funkcją Lamberta, ponieważ zagadnienia z nią
związane rozważane były już przez osiemnastowiecznego matematyka
Johanna Heinricha Lamberta (a także przez Eulera). Przydaje się ona do opisu
rozwiązań ważnych w zastosowaniach równań różniczkowych
z opóźnieniem i niektórych równań fizyki kwantowej, a także, jako
funkcja tworząca, w kombinatoryce. Czytelnik zechce sprawdzić, że
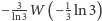 jest rozwiązaniem równania
jest rozwiązaniem równania
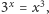 i ustalić,
czy liczba ta jest mniejsza od 3.
i ustalić,
czy liczba ta jest mniejsza od 3.
Udowodnimy, że
Twierdzenie. Dla liczb zespolonych
 dostatecznie bliskich zera
(można też ograniczyć się do
dostatecznie bliskich zera
(można też ograniczyć się do
 rzeczywistych bez potrzeby
wprowadzania zmian w dowodzie) funkcję
rzeczywistych bez potrzeby
wprowadzania zmian w dowodzie) funkcję
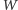 można przedstawić
w postaci szeregu potęgowego
można przedstawić
w postaci szeregu potęgowego

gdzie
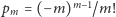 – ponieważ
– ponieważ
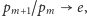 gdy
gdy
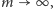 więc dla wszystkich
więc dla wszystkich
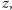 dla
których
dla
których
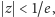 szereg ten jest zbieżny.
szereg ten jest zbieżny.
Trzeba wykazać, że dla powyższego szeregu
 równość
równość
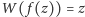 jest spełniona dla wszystkich
jest spełniona dla wszystkich
 z pewnego otoczenia
zera. Przyda się nam prosta tożsamość kombinatoryczna.
z pewnego otoczenia
zera. Przyda się nam prosta tożsamość kombinatoryczna.
Dowód lematu. Rozważmy funkcje
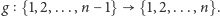 Dla
Dla
 niech
niech
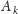 oznacza
oznacza
 czyli rodzinę tych funkcji
ze zbioru
czyli rodzinę tych funkcji
ze zbioru
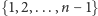 w zbiór
w zbiór
 które nie przyjmują
wartości
które nie przyjmują
wartości
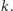 Dla dowolnych
Dla dowolnych
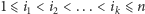 mamy
mamy

Żadna z funkcji określonych na zbiorze
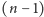 -elementowym nie może
przyjmować
-elementowym nie może
przyjmować
 różnych wartości, więc
różnych wartości, więc
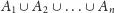 to
rodzina wszystkich funkcji ze zbioru
to
rodzina wszystkich funkcji ze zbioru
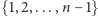 w zbiór
w zbiór
 Zatem ze wzoru włączeń-wyłączeń wnioskujemy,
że
Zatem ze wzoru włączeń-wyłączeń wnioskujemy,
że
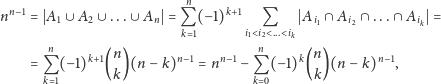
a to już jest równoważne dowodzonej tezie.
Niech teraz
 będzie taką liczbą dodatnią, że
będzie taką liczbą dodatnią, że
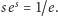 Jeśli
Jeśli
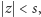 to
to
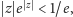 więc
więc
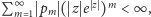 co usprawiedliwia
zmianę kolejności sumowania:
co usprawiedliwia
zmianę kolejności sumowania:
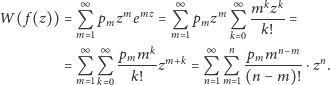
Skorzystaliśmy tu ze znanego rozwinięcia funkcji wykładniczej w szereg
potęgowy,
 a następnie pogrupowaliśmy składniki
według potęg parametru
a następnie pogrupowaliśmy składniki
według potęg parametru
 Współczynnik przy
Współczynnik przy
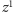 jest
równy
jest
równy
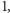 a dla
a dla
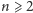 mamy
mamy

na mocy lematu. Zatem wykazaliśmy, że
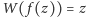 dla wszystkich
liczb zespolonych
dla wszystkich
liczb zespolonych
 z koła otwartego o środku w zerze i promieniu
z koła otwartego o środku w zerze i promieniu
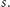 Zawiera się ono w spójnym podzbiorze otwartym płaszczyzny
zespolonej
Zawiera się ono w spójnym podzbiorze otwartym płaszczyzny
zespolonej

Czytelnik obeznany nieco z teorią funkcji analitycznych bez problemu wywnioskuje
stąd, że
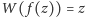 dla
dla
 a więc w szczególności
dla
a więc w szczególności
dla
 Przechodząc do granicy
Przechodząc do granicy
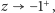 otrzymamy też
równość
otrzymamy też
równość
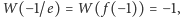 czyli
czyli
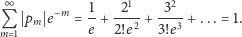
Omówione rozwinięcie funkcji
 w szereg to szczególny przypadek
nieco bardziej skomplikowanego klasycznego wzoru Lagrange’a –
jeśli
w szereg to szczególny przypadek
nieco bardziej skomplikowanego klasycznego wzoru Lagrange’a –
jeśli
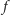 rozwija się w szereg potęgowy na pewnym otoczeniu
zera, a ponadto
rozwija się w szereg potęgowy na pewnym otoczeniu
zera, a ponadto
 i
i
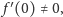 to istnieje funkcja
analityczna
to istnieje funkcja
analityczna
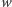 rozwijalna na pewnym otoczeniu zera w szereg
rozwijalna na pewnym otoczeniu zera w szereg
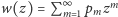 i taka, że
i taka, że
 dla
dla
 dostatecznie
bliskich zera, a przy tym
dostatecznie
bliskich zera, a przy tym
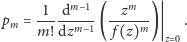
Gdy
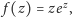 to
to
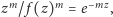 skąd łatwo otrzymać
współczynniki funkcji Lamberta.
skąd łatwo otrzymać
współczynniki funkcji Lamberta.
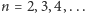
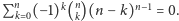
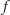 określoną takim samym wzorem, ale na całej płaszczyźnie
zespolonej
określoną takim samym wzorem, ale na całej płaszczyźnie
zespolonej
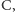 na której nie jest już ona różnowartościowa,
w związku z czym funkcję odwrotną do niej trzeba definiować lokalnie;
wprowadzona przez nas funkcja
na której nie jest już ona różnowartościowa,
w związku z czym funkcję odwrotną do niej trzeba definiować lokalnie;
wprowadzona przez nas funkcja
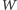 to tylko fragment jednej z gałęzi
funkcji Lamberta.
to tylko fragment jednej z gałęzi
funkcji Lamberta.
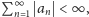 to wyrazy
szeregu
to wyrazy
szeregu
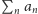 można dowolnie przestawiać bez wpływu na wynik
sumowania.
można dowolnie przestawiać bez wpływu na wynik
sumowania.
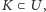 gdzie
gdzie
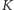 jest
kołem otwartym, a
jest
kołem otwartym, a
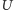 pewnym spójnym otwartym podzbiorem
płaszczyzny zespolonej. Jeśli funkcje analityczne
pewnym spójnym otwartym podzbiorem
płaszczyzny zespolonej. Jeśli funkcje analityczne
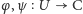 spełniają
równość
spełniają
równość
 dla wszystkich
dla wszystkich
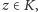 to
to
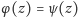 dla wszystkich
dla wszystkich
