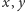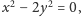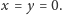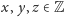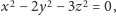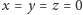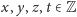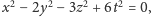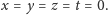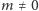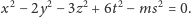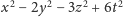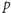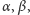Niewymierność
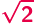 i jeszcze większe
niemożliwości
i jeszcze większe
niemożliwości
Punktem wyjścia niech będzie najsłynniejsza chyba matematyczna konstatacja,
ta mianowicie, że liczba
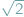 jest niewymierna...
jest niewymierna...
Można to wysłowić w następujący równoważny i tendencyjny sposób.
Czy twierdzenie to można wzmocnić? Okazuje się, że tak! Zachodzi mianowicie
Zauważmy przede wszystkim, że jeśli liczba całkowita
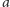 nie dzieli
się przez
nie dzieli
się przez
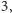
to
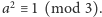 Ponieważ
Ponieważ
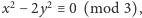 więc
więc
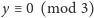 oraz
oraz
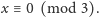 Zatem
Zatem
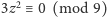 i stąd
również
i stąd
również
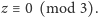 Istnieją więc takie liczby całkowite
Istnieją więc takie liczby całkowite
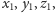 że
że
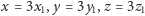 oraz
oraz
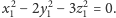 Wynika stąd, że
wyjściowe liczby
Wynika stąd, że
wyjściowe liczby
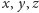 są podzielne przez dowolnie wysokie potęgi
liczby
są podzielne przez dowolnie wysokie potęgi
liczby
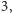 a to jest możliwe tylko dla
a to jest możliwe tylko dla
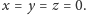
Okazuje się, że można to jeszcze bardziej uogólnić!
Z równości
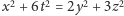 wynika bowiem, że
wynika bowiem, że

Z twierdzenia 2 wynika teraz, że
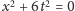 i stąd
i stąd
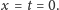 Z równości
Z równości
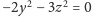 otrzymujemy ostatecznie
otrzymujemy ostatecznie
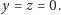
Jak Czytelnik słusznie przeczuwa, niemożliwości nie mogą rozpychać się w nieskończoność, a w naszym przypadku przygważdża je
Łatwo zauważyć, że powyższe twierdzenie można wypowiedzieć w następujący równoważny sposób:
Twierdzenie. Dla każdej liczby całkowitej
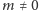 istnieją takie liczby
wymierne
istnieją takie liczby
wymierne
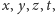 że
że

Kluczowy jest poniższy lemat.
Dowód wynika z następujących tożsamości:
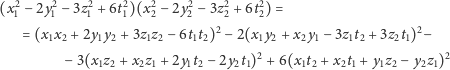 |
oraz

gdzie oznaczyliśmy
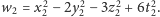
Z lematu 1 wynika przede wszystkim, że dla dowodu twierdzenia 4 wystarczy
rozpatrzyć tylko przypadek
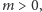 gdyż
gdyż

Dowód przeprowadzimy przez indukcję ze względu na
 Dla
Dla
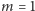 oraz
oraz
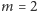 mamy przedstawienia
mamy przedstawienia

Załóżmy z kolei, że
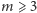 i teza zachodzi dla
i teza zachodzi dla
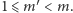 Rozróżniamy
teraz dwa przypadki. Jeżeli
Rozróżniamy
teraz dwa przypadki. Jeżeli
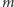 jest liczbą złożoną, to
jest liczbą złożoną, to
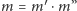 gdzie
gdzie
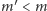 oraz
oraz
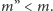 Z lematu 1 wynika więc odpowiednie
przedstawienie dla
Z lematu 1 wynika więc odpowiednie
przedstawienie dla
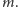 Jeżeli
Jeżeli
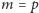 jest liczbą pierwszą, to sytuacja
jest bardziej skomplikowana. Przyda się następujący
jest liczbą pierwszą, to sytuacja
jest bardziej skomplikowana. Przyda się następujący
Załóżmy od razu, że
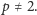 Reszty mod
Reszty mod
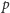 liczb
liczb

są parami różne i jest ich
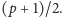 Podobnie, reszty mod
Podobnie, reszty mod
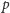 liczb
liczb

są parami różne i jest ich
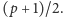 Ponieważ wszystkich reszt mod
Ponieważ wszystkich reszt mod
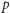 jest tylko
jest tylko
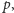 więc pewna reszta typu
więc pewna reszta typu
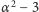 pokrywa się
z pewną resztą typu
pokrywa się
z pewną resztą typu
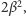 co daje tezę lematu 2.
co daje tezę lematu 2.
Ponieważ
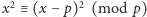 więc w lemacie 2 możemy
założyć, że liczby całkowite
więc w lemacie 2 możemy
założyć, że liczby całkowite
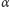 i
i
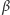 spełniają dodatkowo
nierówności
spełniają dodatkowo
nierówności

Mamy zatem oszacowania

Ponieważ
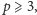 więc
więc

Możemy zatem napisać

Na mocy założenia indukcyjnego liczba naturalna
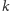 ma przedstawienie
ma przedstawienie

Wnosimy stąd na podstawie lematu 1, że liczba

też ma takie przedstawienie i to kończy dowód indukcyjny twierdzenia.
Wyniki przedstawione powyżej są kompletne, ale dość sztuczne. Szczęście
nam sprzyjało, gdyż forma kwadratowa
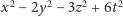 jest tzw.
formą normową dla algebry kwaternionowej
jest tzw.
formą normową dla algebry kwaternionowej
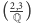 – stąd wynika
„cudowna” tożsamość wypisana w Lemacie 1. A gdyby nie pomagać
szczęściu aż tak bardzo? Okazuje się, że prawdziwe jest następujące ogólne
twierdzenie.
– stąd wynika
„cudowna” tożsamość wypisana w Lemacie 1. A gdyby nie pomagać
szczęściu aż tak bardzo? Okazuje się, że prawdziwe jest następujące ogólne
twierdzenie.
Twierdzenie 5. Jeżeli liczby wymierne
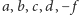 są różne od
zera oraz nie są wszystkie tego samego znaku to istnieją takie liczby wymierne
są różne od
zera oraz nie są wszystkie tego samego znaku to istnieją takie liczby wymierne
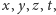 że
że

Dowód tego twierdzenia wymaga zastosowania poważnej i pięknej matematyki. Ważnymi jego składnikami są: prawo wzajemności dla reszt kwadratowych oraz twierdzenie Dirichleta o liczbach pierwszych w postępie arytmetycznym. To wszystko, i dużo więcej, znajdzie Czytelnik w zajmującej książce: Z.I. Borewicz, I.R. Szafarewicz, Теория чисел, Moskwa 1985 (istnieją tłumaczenia na angielski i niemiecki).