Człapanie do nieskończoności
Matematyka, jak przystało na królową nauk, jest dyscypliną dość trudną i wymagającą umiejętności abstrakcyjnego myślenia. Jeżeli przyjąć za Galileuszem, że matematyka jest alfabetem, za pomocą którego Bóg opisał wszechświat, to trzeba przyznać, że jest to alfabet dość złożony i nie jest łatwo nauczyć się dobrze nim posługiwać. Jednym z jego ważniejszych elementów jest niewątpliwie nieskończoność.
Próba zrozumienia nieskończoności dla człowieka, który w istocie rzeczy żyje otoczony wielkościami skończonymi (a przynajmniej takie mu się one na pierwszy rzut oka wydają), często opiera się na swoistym przeniesieniu doświadczeń czy intuicji znanych mu z jego „skończonego” świata, co zwykle kończy się niepowodzeniem. Dobrym tego przykładem są szeregi, czyli obiekty matematyczne, które (niezbyt precyzyjnie pisząc) uogólniają pojęcie sumy na przypadek nieskończenie wielu składników.
Już ze szkoły średniej wiadomo, że taka uogólniona suma nieskończonej
ilości dodatnich składników może być skończona (przekonuje o tym
chociażby wzór na sumę składników nieskończonego ciągu geometrycznego
o ilorazie
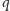 w przypadku, gdy
w przypadku, gdy
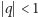 ). Gdy pojawia się zatem
problem obliczenia sumy odwrotności wszystkich liczb naturalnych, czyli
szeregu
). Gdy pojawia się zatem
problem obliczenia sumy odwrotności wszystkich liczb naturalnych, czyli
szeregu
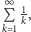 intuicja podparta wyliczeniem kilku jego początkowych
sum częściowych sugeruje, że wielkość ta jest skończona, a nawet
niezbyt duża. To podejrzenie wzmacnia użycie dowolnego kalkulatora czy
komputera – od pewnego momentu pojawiające się na ich ekranach sumy
częściowe
intuicja podparta wyliczeniem kilku jego początkowych
sum częściowych sugeruje, że wielkość ta jest skończona, a nawet
niezbyt duża. To podejrzenie wzmacnia użycie dowolnego kalkulatora czy
komputera – od pewnego momentu pojawiające się na ich ekranach sumy
częściowe
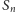 nie ulegają zmianie. Czy zatem rzeczywiście szereg
nie ulegają zmianie. Czy zatem rzeczywiście szereg
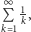 zwany szeregiem harmonicznym, jest zbieżny? Otóż nie! Co
więcej, nawet nietrudno to wykazać. Wystarczy w tym celu zauważyć, że
pewne sumy częściowe szeregu harmonicznego łatwo oszacować z dołu
w następujący sposób:
zwany szeregiem harmonicznym, jest zbieżny? Otóż nie! Co
więcej, nawet nietrudno to wykazać. Wystarczy w tym celu zauważyć, że
pewne sumy częściowe szeregu harmonicznego łatwo oszacować z dołu
w następujący sposób:

a otrzymane dolne oszacowanie przy
 dąży przecież do
nieskończoności.
dąży przecież do
nieskończoności.
Wiemy już, że szereg harmoniczny jest rozbieżny, w jaki sposób możemy
jednak znaleźć liczbę składników
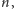 dla których
dla których
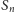 przekroczy
zadaną z góry liczbę? Próba odpowiedzi na to pytanie poprzez zwyczajne
dodawanie kolejnych składników naszego szeregu nie zaprowadzi nas daleko,
nawet jeśli wspomożemy się komputerem. Z pomocą przyjdzie nam,
oczywiście, matematyka, a konkretnie całki. Zauważmy bowiem, że dla
dowolnego
przekroczy
zadaną z góry liczbę? Próba odpowiedzi na to pytanie poprzez zwyczajne
dodawanie kolejnych składników naszego szeregu nie zaprowadzi nas daleko,
nawet jeśli wspomożemy się komputerem. Z pomocą przyjdzie nam,
oczywiście, matematyka, a konkretnie całki. Zauważmy bowiem, że dla
dowolnego
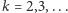 oraz
oraz
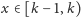 mamy oczywistą
nierówność
mamy oczywistą
nierówność
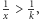 zachodzi więc również
zachodzi więc również
 |
a zatem
 |
W analogiczny sposób, biorąc jako punkt wyjścia nierówność
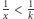 prawdziwą dla każdego
prawdziwą dla każdego
 możemy
otrzymać
możemy
otrzymać
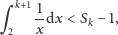 |
co ostatecznie prowadzi do następującego oszacowania sum częściowych
 szeregu harmonicznego:
szeregu harmonicznego:
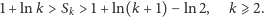 | (1) |
Co więcej, można również wykazać, że przy
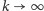 istnieje
skończona granica ciągu
istnieje
skończona granica ciągu
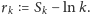 Wynika to z faktu, że
ciąg
Wynika to z faktu, że
ciąg
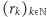 jest ściśle malejący, o czym świadczy poniższy
rachunek
jest ściśle malejący, o czym świadczy poniższy
rachunek
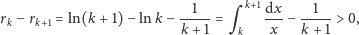 |
oraz ograniczony, gdyż z (1) otrzymujemy
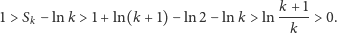 |
Oznaczając jego granicę przez
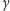 i ponownie wykorzystując
monotoniczność ciągu
i ponownie wykorzystując
monotoniczność ciągu
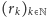 oraz (1), możemy zapisać
oraz (1), możemy zapisać
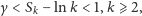 | (2) |
Ostatnia nierówność mówi nam, że w praktyce
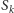 dość
dokładnie można przybliżyć przez
dość
dokładnie można przybliżyć przez
 Stała
Stała
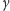 pełni na tyle
istotną rolę w matematyce, że otrzymała nawet swoją nazwę (nazywa się ją stałą
Eulera bądź czasami stałą Eulera–Mascheroniego). W porównaniu
z dwiema najsłynniejszymi stałymi, czyli
pełni na tyle
istotną rolę w matematyce, że otrzymała nawet swoją nazwę (nazywa się ją stałą
Eulera bądź czasami stałą Eulera–Mascheroniego). W porównaniu
z dwiema najsłynniejszymi stałymi, czyli
 oraz
oraz
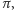 nadal
niezbyt wiele o niej wiadomo (kwestią otwartą jest chociażby to, czy
nadal
niezbyt wiele o niej wiadomo (kwestią otwartą jest chociażby to, czy
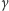 jest liczbą algebraiczną; nie wiadomo nawet, czy jest ona liczbą
wymierną).
jest liczbą algebraiczną; nie wiadomo nawet, czy jest ona liczbą
wymierną).
Korzystając z (1), łatwo oszacować sumę kolejnych składników szeregu
harmonicznego. I tak, na przykład,
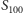 znajduje się między
znajduje się między
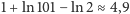 a
a
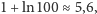 zaś
zaś
 między
między
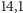 a
a
 Podobnie łatwo oszacować, ile trzeba dodać
kolejnych składników tego szeregu, aby przekroczyć ustaloną wartość.
Jak Czytelnik sądzi, kiedy
Podobnie łatwo oszacować, ile trzeba dodać
kolejnych składników tego szeregu, aby przekroczyć ustaloną wartość.
Jak Czytelnik sądzi, kiedy
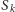 przekroczy
przekroczy
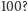 Stanie się
to, gdy dodamy mniej więcej
Stanie się
to, gdy dodamy mniej więcej
 pierwszych składników
szeregu harmonicznego. To naprawdę ogromna liczba. Nawet najszybszy
polski superkomputer, Zeus, o mocy obliczeniowej równej mniej więcej
pierwszych składników
szeregu harmonicznego. To naprawdę ogromna liczba. Nawet najszybszy
polski superkomputer, Zeus, o mocy obliczeniowej równej mniej więcej
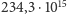 operacji zmiennoprzecinkowych wykonywanych na sekundę,
musiałby obliczać tę sumę (przy założeniu, że dodanie dwóch kolejnych
składników to jedna operacja) bez przerwy przez... około
operacji zmiennoprzecinkowych wykonywanych na sekundę,
musiałby obliczać tę sumę (przy założeniu, że dodanie dwóch kolejnych
składników to jedna operacja) bez przerwy przez... około
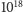 lat (wiek
Wszechświata szacuje się raptem na
lat (wiek
Wszechświata szacuje się raptem na
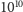 lat)! Ta bardzo wolna
rozbieżność szeregu harmonicznego jest jedną z jego wielu interesujących
własności.
lat)! Ta bardzo wolna
rozbieżność szeregu harmonicznego jest jedną z jego wielu interesujących
własności.
Nasuwa się naturalne pytanie: czy w klasie szeregów o dodatnich wyrazach
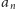 istnieją może jeszcze wolniej rozbieżne szeregi? Nim odpowiemy na
to pytanie, musimy sprecyzować, co będziemy rozumieli pod pojęciem
wolniejszej rozbieżności. Niech zatem dane będą dwa szeregi rozbieżne
istnieją może jeszcze wolniej rozbieżne szeregi? Nim odpowiemy na
to pytanie, musimy sprecyzować, co będziemy rozumieli pod pojęciem
wolniejszej rozbieżności. Niech zatem dane będą dwa szeregi rozbieżne
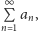
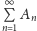 o wyrazach dodatnich. Powiemy, że szereg
o wyrazach dodatnich. Powiemy, że szereg
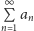 jest wolniej rozbieżny niż szereg
jest wolniej rozbieżny niż szereg
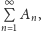 jeżeli
jeżeli
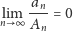 |
(czyli od pewnego indeksu wyrazy pierwszego szeregu będą „znacząco” mniejsze od wyrazów drugiego). Okazuje się, że w rozważanej przez nas klasie możemy konstruować szeregi tak wolno zmierzające ku nieskończoności, jak tylko chcemy. Swoistą „maszynką” do ich tworzenia jest bowiem następujące twierdzenie, pochodzące od Abela i Diniego:
Twierdzenie 1.
Jeżeli szereg
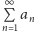 o wyrazach dodatnich jest rozbieżny, to szereg
o wyrazach dodatnich jest rozbieżny, to szereg
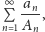 gdzie
gdzie
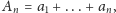 również jest rozbieżny
i to wolniej.
również jest rozbieżny
i to wolniej.
Powyższe twierdzenie orzeka w szczególności, że nie istnieje szereg „najwolniej” rozbieżny.
Zapewne najbardziej znaną rodzinę coraz wolniej rozbieżnych szeregów tworzą
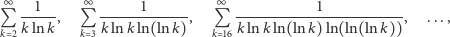 |
czyli, po przenumerowaniu składników, szeregi
Aby uwidocznić, jak wolno ich sumy częściowe zbiegają do
nieskończoności, wystarczy ponownie przeprowadzić rozumowanie, które
pozwoliło nam uzyskać wzór (2) dla szeregu harmonicznego (zauważmy, że
w każdym z przypadków funkcje pod znakiem szeregu są ściśle
malejące). Otrzymamy wówczas następujące oszacowania sum częściowych
 pierwszych trzech szeregów tej rodziny, prawdziwe dla
pierwszych trzech szeregów tej rodziny, prawdziwe dla
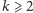 :
:
- dla szeregu (S1)
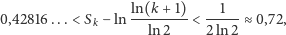
- dla szeregu (S2)

- dla szeregu (S3)
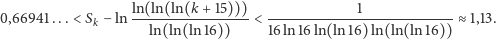
Co z nich wynika? Przede wszystkim to, że pojęcie wolnej rozbieżności jest
bardzo względne. Szereg harmoniczny, który dąży do nieskończoności
w niesamowicie wolnym, wydawałoby się, tempie, przy szeregach (S1)–(S3)
zdaje się do niej pędzić wręcz z zawrotną prędkością. Przykładowo,
wartość
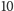 szereg (S1) przekroczy dopiero po dodaniu około
szereg (S1) przekroczy dopiero po dodaniu około
 początkowych swoich wyrazów, zaś szereg (S2) – po
zsumowaniu aż
początkowych swoich wyrazów, zaś szereg (S2) – po
zsumowaniu aż
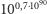 początkowych wyrazów. Dla porównania
szereg harmoniczny potrzebuje na to zaledwie
początkowych wyrazów. Dla porównania
szereg harmoniczny potrzebuje na to zaledwie
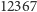 składników. Co
ciekawe, to „człapanie” do nieskończoności szeregów (S1)–(S3), a także
pozostałych członków tej rodziny, jest tak wolne, że gdy tylko odpowiednio
zmniejszymy ich składniki, czyli utworzymy nową rodzinę szeregów
postaci
składników. Co
ciekawe, to „człapanie” do nieskończoności szeregów (S1)–(S3), a także
pozostałych członków tej rodziny, jest tak wolne, że gdy tylko odpowiednio
zmniejszymy ich składniki, czyli utworzymy nową rodzinę szeregów
postaci

dla dowolnego
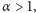 to w końcu zatrzymają się one w swym
powolnym marszu ku nieskończoności i staną się zbieżne. Z jednej strony
jest to na pewno zaskakujący rezultat, gdyż, na przykład, szeregi
to w końcu zatrzymają się one w swym
powolnym marszu ku nieskończoności i staną się zbieżne. Z jednej strony
jest to na pewno zaskakujący rezultat, gdyż, na przykład, szeregi
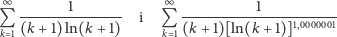 |
nie wydają się zbytnio różnić na pierwszy rzut oka. Jednakże z drugiej strony, jak już wspomnieliśmy, nasze intuicje w zderzeniu z pojęciem nieskończoności często okazują się błędne. Jest to jednak zrozumiałe, w końcu nawet sam Abel, który był genialnym matematykiem i jak niewielu rozumiał ten „boski alfabet”, powiedział przecież, że „rozbieżne szeregi są diabelskim wynalazkiem”.

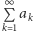 jest zbieżny, gdy istnieje skończona granica
ciągu sum częściowych
jest zbieżny, gdy istnieje skończona granica
ciągu sum częściowych
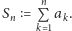
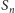 nie ma skończonej granicy, szereg nazwiemy
rozbieżnym.
nie ma skończonej granicy, szereg nazwiemy
rozbieżnym.