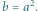Nieznane wykresy znanych funkcji
Zaczęło się od okręgu. Wykres funkcji sinus okazał się okręgiem. Jak to możliwe? Okazuje się, że czasem lekkie odstąpienie od utartego punktu widzenia może nas daleko zaprowadzić. Wystarczy, na przykład, wybrać inny niż prostokątny układ współrzędnych do przedstawiania wykresów funkcji.
Pierwszym układem współrzędnych, jaki nasuwa nam się zamiast układu
prostokątnego, jest układ biegunowy. Dla przypomnienia, w tym układzie punkt
o współrzędnych
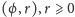 leży na półprostej tworzącej z ustaloną
osią biegunową kąt skierowany o mierze
leży na półprostej tworzącej z ustaloną
osią biegunową kąt skierowany o mierze
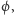 w odległości
w odległości
 od
ustalonego bieguna. Dla ujemnych wartości
od
ustalonego bieguna. Dla ujemnych wartości
 przyjmujemy, że punkt
leży po przeciwnej stronie bieguna, czyli że
przyjmujemy, że punkt
leży po przeciwnej stronie bieguna, czyli że
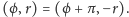
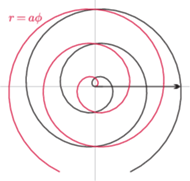
Rys. 1 Wykres funkcji liniowej we współrzędnych biegunowych, złożony z dwóch spiral Archimedesa
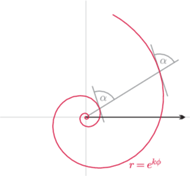
Rys. 2 Spirala logarytmiczna
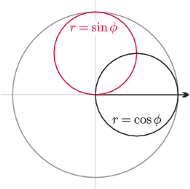
Rys. 3 Wykresy funkcji sinus (kolorowy) i cosinus (czarny) w układzie biegunowym
Dopuszczenie miar kąta spoza przedziału
 oraz ujemnych wartości
promienia powoduje, że układ biegunowy przestaje spełniać klasyczną
definicję układu współrzędnych – przyporządkowanie współrzędnych
punktowi przestaje być jednoznaczne. Z punktu widzenia zastosowania układu
biegunowego do przedstawiania wykresów funkcji oznacza to, że z takiego
wykresu nie da się odczytywać wartości funkcji.
oraz ujemnych wartości
promienia powoduje, że układ biegunowy przestaje spełniać klasyczną
definicję układu współrzędnych – przyporządkowanie współrzędnych
punktowi przestaje być jednoznaczne. Z punktu widzenia zastosowania układu
biegunowego do przedstawiania wykresów funkcji oznacza to, że z takiego
wykresu nie da się odczytywać wartości funkcji.
Przyjrzyjmy się wykresom kilku elementarnych funkcji w układzie
biegunowym. Na początek przyjmijmy, że zmienną niezależną jest kąt
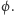 Wykres funkcji liniowej
Wykres funkcji liniowej
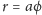 okazuje się spiralą Archimedesa
(Rys. 1). Wykresem funkcji wykładniczej
okazuje się spiralą Archimedesa
(Rys. 1). Wykresem funkcji wykładniczej
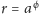 jest zaś spirala
logarytmiczna (Rys. 2), przecinająca wszystkie półproste wychodzące
z bieguna pod jednakowym kątem. Wykresy funkcji trygonometrycznych
sinus
jest zaś spirala
logarytmiczna (Rys. 2), przecinająca wszystkie półproste wychodzące
z bieguna pod jednakowym kątem. Wykresy funkcji trygonometrycznych
sinus
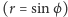 i cosinus
i cosinus
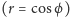 przybiorą kształt
okręgów (Rys. 3). Funkcje trygonometryczne, a także funkcje budowane na
ich podstawie, dają zwykle ciekawe wykresy w układzie biegunowym.
Na przykład
przybiorą kształt
okręgów (Rys. 3). Funkcje trygonometryczne, a także funkcje budowane na
ich podstawie, dają zwykle ciekawe wykresy w układzie biegunowym.
Na przykład
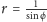 to prosta, a
to prosta, a
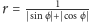 to brzeg
kwadratu.
to brzeg
kwadratu.
Zachęcam do własnych badań nad wykresami funkcji
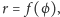 a także
funkcji
a także
funkcji
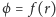 – zwykle otrzymujemy wtedy zupełnie inne rezultaty.
– zwykle otrzymujemy wtedy zupełnie inne rezultaty.
Abstrahując od konkretnych funkcji, możemy także zastanowić się nad
ogólniejszymi własnościami. Na przykład wykres każdej funkcji nieparzystej
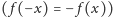 we współrzędnych biegunowych jest symetryczny
względem prostej prostopadłej do osi biegunowej. Wykres funkcji parzystej
we współrzędnych biegunowych jest symetryczny
względem prostej prostopadłej do osi biegunowej. Wykres funkcji parzystej
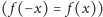 jest z kolei symetryczny względem osi biegunowej. Fakty
te można stosunkowo prosto wykazać, korzystając z zależności między
współrzędnymi biegunowymi a prostokątnymi.
jest z kolei symetryczny względem osi biegunowej. Fakty
te można stosunkowo prosto wykazać, korzystając z zależności między
współrzędnymi biegunowymi a prostokątnymi.
Z tematem niekonwencjonalnych wykresów funkcji wiąże się jeszcze (co
najmniej) jeden ciekawy okrąg. Nazwałem go okręgiem liczbowym, gdyż
każdemu jego punktowi odpowiada liczba rzeczywista. Konstrukcja
okręgu liczbowego opiera się na rzucie stereograficznym. Okrąg
o jednostkowej średnicy jest styczny do osi liczbowej w jej początku.
Punkt
 o współrzędnej
o współrzędnej
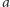 na okręgu liczbowym leży
na odcinku łączącym punkt o współrzędnej
na okręgu liczbowym leży
na odcinku łączącym punkt o współrzędnej
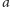 na osi liczbowej
z punktem antypodycznym do punktu styczności (środkiem rzutu
stereograficznego). Samemu środkowi rzutu przyporządkowujemy wartość
na osi liczbowej
z punktem antypodycznym do punktu styczności (środkiem rzutu
stereograficznego). Samemu środkowi rzutu przyporządkowujemy wartość

Tak zdefiniowany okrąg liczbowy ma dość interesujące własności. Na wstępie
warto zauważyć, że liczba przypisana danemu punktowi
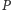 na okręgu
jest tak naprawdę równa
na okręgu
jest tak naprawdę równa
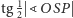 (patrz Rys. 4). Korzystając ze
wzorów redukcyjnych, można wykazać, że średnica okręgu liczbowego
łączy ze sobą punkty odpowiadające liczbom, których iloczyn wynosi
(patrz Rys. 4). Korzystając ze
wzorów redukcyjnych, można wykazać, że średnica okręgu liczbowego
łączy ze sobą punkty odpowiadające liczbom, których iloczyn wynosi
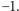 Ponadto każda liczba dodatnia i jej odwrotność są równoodległe
od
Ponadto każda liczba dodatnia i jej odwrotność są równoodległe
od
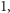 a liczba ujemna i jej odwrotność – równoodległe od
a liczba ujemna i jej odwrotność – równoodległe od
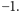
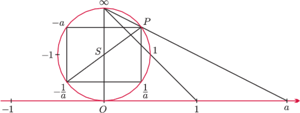
Rys. 4 Konstrukcja okręgu liczbowego
Jaki jest związek okręgu liczbowego z wykresami funkcji? Jak sama nazwa
wskazuje, można go wykorzystać zamiast osi liczbowej i skonstruować
całkiem ciekawy układ współrzędnych na nieograniczonej powierzchni
walcowej. W takim układzie jedna oś współrzędnych jest klasyczną osią
liczbową pokrywającą się z jedną z tworzących, a drugą oś stanowi
okrąg liczbowy ułożony prostopadle do tworzących. W takim układzie
współrzędnych wykres funkcji odwrotność, czyli
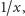 okazuje się
spójną krzywą (jeśli przyjmiemy, że dla argumentu
okazuje się
spójną krzywą (jeśli przyjmiemy, że dla argumentu
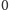 funkcja
odwrotność jest określona i przyjmuje wartość
funkcja
odwrotność jest określona i przyjmuje wartość
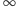 ).
).
Dla uproszczenia, możemy sobie wyobrazić (Rys. 5), że rozcinamy
powierzchnię walca wzdłuż prostej o rzędnej równej
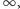 otrzymując
pas bez brzegu (przy okazji pozbywamy się kontrowersyjnej liczby
otrzymując
pas bez brzegu (przy okazji pozbywamy się kontrowersyjnej liczby
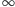 ).
W swojej pracy nazwałem przyporządkowanie parom liczb rzeczywistych
punktów takiego pasa Y-ograniczonym odwzorowaniem współrzędnych.
Formalnie, odwzorowanie Y-ograniczone przyporządkowuje parze liczb
rzeczywistych
).
W swojej pracy nazwałem przyporządkowanie parom liczb rzeczywistych
punktów takiego pasa Y-ograniczonym odwzorowaniem współrzędnych.
Formalnie, odwzorowanie Y-ograniczone przyporządkowuje parze liczb
rzeczywistych
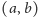 punkt płaszczyzny o współrzędnych prostokątnych
punkt płaszczyzny o współrzędnych prostokątnych
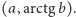
W odwzorowaniu Y-ograniczonym wykresy niektórych funkcji zyskują wartość estetyczną, której nie przejawiają przy przedstawianiu w układzie prostokątnym. Na przykład wykres funkcji tangens w takim odwzorowaniu składa się z prostych odcinków, które po nawinięciu wykresu na walec (i uzupełnieniu funkcji tangens o wartości nieskończone w punktach nieokreśloności) tworzą linię śrubową. Wynika to, oczywiście, z wykorzystania funkcji tangens do konstrukcji odwzorowania Y-ograniczonego.
Najciekawszym (i jednocześnie prostym) przykładem wydaje mi się jednak
funkcja wykładnicza. Jej wykres w odwzorowaniu Y-ograniczonym ma środek
symetrii w punkcie
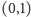 przecięcia z „osią” rzędnych (Rys. 6). Wynika
to z faktu, że
przecięcia z „osią” rzędnych (Rys. 6). Wynika
to z faktu, że
 zatem jeśli punkt
zatem jeśli punkt
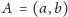 należy do
wykresu, punkt
należy do
wykresu, punkt
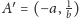 również do niego należy. Zgodnie
z własnościami okręgu liczbowego wzajemnie odwrotne liczby dodatnie są
równoodległe od
również do niego należy. Zgodnie
z własnościami okręgu liczbowego wzajemnie odwrotne liczby dodatnie są
równoodległe od
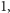 czyli punkty
czyli punkty
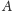 i
i
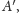 które
są równoodległe od punktu
które
są równoodległe od punktu
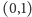 w poziomie, będą od niego
równoodległe także w pionie, czyli są środkowo symetryczne względem
w poziomie, będą od niego
równoodległe także w pionie, czyli są środkowo symetryczne względem
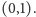 Ponieważ każdy punkt wykresu należy do niego wraz ze swym
obrazem w symetrii względem
Ponieważ każdy punkt wykresu należy do niego wraz ze swym
obrazem w symetrii względem
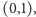 więc cały wykres jest środkowo
symetryczny.
więc cały wykres jest środkowo
symetryczny.
W ograniczaniu obszaru wykresu można posunąć się jeszcze dalej. Gdy obie
osie prostokątnego układu współrzędnych zastąpimy rozciętymi okręgami
liczbowymi – otrzymamy odwzorowanie XY-ograniczone. Przeciwdziedziną
XY-ograniczonego odwzorowania współrzędnych jest kwadrat o boku
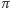 (bez brzegu). Zgodnie z formalną definicją, w tym odwzorowaniu
parze liczb
(bez brzegu). Zgodnie z formalną definicją, w tym odwzorowaniu
parze liczb
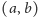 odpowiada punkt płaszczyzny o współrzędnych
prostokątnych
odpowiada punkt płaszczyzny o współrzędnych
prostokątnych
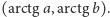 Odwzorowanie XY-ograniczone daje
nam możliwość przedstawienia (na ograniczonej powierzchni) wykresu
funkcji w całym zbiorze liczb rzeczywistych.
Odwzorowanie XY-ograniczone daje
nam możliwość przedstawienia (na ograniczonej powierzchni) wykresu
funkcji w całym zbiorze liczb rzeczywistych.
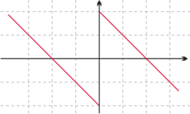
Rys. 7 Wykres funkcji odwrotność w odwzorowaniu XY-ograniczonym.
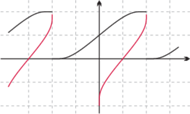
Rys. 8 Wykresy przykładowych funkcji wykładniczej (czarny) i logarytmicznej (kolorowy) w odwzorowaniu XY-ograniczonym.
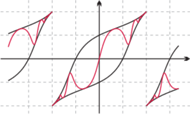
Rys. 9 Wykres funkcji
 ograniczony krzywymi
ograniczony krzywymi
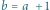 i
i
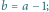 odwzorowanie XY-ograniczone zachowuje punkty przecięcia
wykresów i pozwala porównywać wartości funkcji.
odwzorowanie XY-ograniczone zachowuje punkty przecięcia
wykresów i pozwala porównywać wartości funkcji.

Rys. 10 Wykres
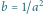 powstały przez odbicie wykresu
powstały przez odbicie wykresu
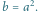
Jako pierwszy przykład wykresu funkcji w odwzorowaniu XY-ograniczonym
rozpatrzmy wykres funkcji odwrotność (Rys. 7). Składa się on z dwóch prostych
odcinków (bez końców). Odcinki te są równoległe do wykresu funkcji
liniowej
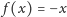 w tym odwzorowaniu, co wynika ze wspomnianej
już własności okręgu liczbowego: liczby
w tym odwzorowaniu, co wynika ze wspomnianej
już własności okręgu liczbowego: liczby
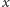 i
i
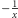 leżą
naprzeciwko siebie, a co za tym idzie, na „rozprostowanym” okręgu liczbowym
odległość pomiędzy
leżą
naprzeciwko siebie, a co za tym idzie, na „rozprostowanym” okręgu liczbowym
odległość pomiędzy
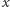 a
a
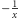 jest stała – równa połowie
długości okręgu. Na tej podstawie wykres funkcji
jest stała – równa połowie
długości okręgu. Na tej podstawie wykres funkcji
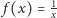 można
otrzymać, przesuwając wykres funkcji
można
otrzymać, przesuwając wykres funkcji
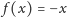 (fragmentami,
oczywiście).
(fragmentami,
oczywiście).
Podobnie jak w odwzorowaniu Y-ograniczonym, tak w XY-ograniczonym
wykres funkcji wykładniczej ma środek symetrii (dowód jest dokładnie taki
sam jak dla odwzorowania Y-ograniczonego). Różnica dotyczy wykresu funkcji
logarytmicznej (o której dotąd nie pisałem), ponieważ w odwzorowaniu
XY-ograniczonym on także ma środek symetrii (w punkcie przecięcia
z „osią” odciętych). Funkcje wzajemnie odwrotne w odwzorowaniu
XY-ograniczonym mają tę samą charakterystyczną cechę co w klasycznym
układzie prostokątnym: są symetryczne względem prostej
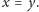
Jeśli punkt wykresu funkcji
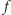 o współrzędnych XY-ograniczonych
o współrzędnych XY-ograniczonych
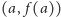 przechodzi na punkt
przechodzi na punkt
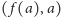 wykresu funkcji
wykresu funkcji
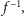 to w przeliczeniu na współrzędne prostokątne punkt
to w przeliczeniu na współrzędne prostokątne punkt
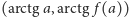 przechodzi na
przechodzi na
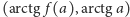 – odbicie
punktu wykresu funkcji
– odbicie
punktu wykresu funkcji
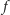 względem prostej
względem prostej
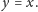
Warto zwrócić uwagę na jeszcze jeden szczegół związany z wykresami
w odwzorowaniach ograniczonych. Wykres funkcji
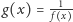 powstaje
przez odbicie symetryczne fragmentu wykresu funkcji
powstaje
przez odbicie symetryczne fragmentu wykresu funkcji
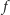 obejmującego
wartości dodatnie oraz fragmentu obejmującego wartości ujemne względem
prostych, odpowiednio,
obejmującego
wartości dodatnie oraz fragmentu obejmującego wartości ujemne względem
prostych, odpowiednio,
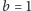 i
i
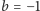 (Rys. 10). Wynika
to, oczywiście, z wielokrotnie tu wspominanych własności okręgu
liczbowego.
(Rys. 10). Wynika
to, oczywiście, z wielokrotnie tu wspominanych własności okręgu
liczbowego.
Moja podróż po świecie niekonwencjonalnych układów współrzędnych prowadziła mnie przez świat niespotykany w szkolnych podręcznikach matematyki. Spirale i zamknięte krzywe będące wykresami funkcji w układzie biegunowym oraz mieszczące się na ograniczonej powierzchni wykresy w odwzorowaniu XY-ograniczonym nie wyczerpują tematu „nieznanych wykresów funkcji”. Zachęcam Czytelnika do zgłębiania tematu niezwykłych wykresów we własnym zakresie. Można analizować różne funkcje, wybrać inne układy współrzędnych, przedstawiać wykresy w przestrzeniach innych niż płaszczyzna euklidesowa... Temat wydaje się niewyczerpany.
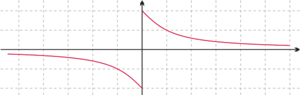
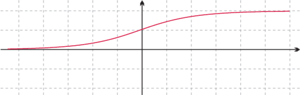
 ograniczony krzywymi
ograniczony krzywymi
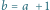 i
i
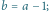 odwzorowanie XY-ograniczone zachowuje punkty przecięcia
wykresów i pozwala porównywać wartości funkcji.
odwzorowanie XY-ograniczone zachowuje punkty przecięcia
wykresów i pozwala porównywać wartości funkcji.
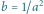 powstały przez odbicie wykresu
powstały przez odbicie wykresu