Gdy się nie ma, co się lubi...
W Delcie 10/2009, w artykule Czy naprawdę prawie robi wielką różnicę, Paulina Małolepsza i Tomasz Małolepszy piszą o przykładach funkcji ciągłych, które są różniczkowalne prawie wszędzie, ale jednak nie są całkami swoich pochodnych.

Funkcja Cantora.

Funkcja Minkowskiego.
Innymi słowy, okazuje się, że w twierdzeniu Newtona–Leibniza, orzekającym,
że jeśli funkcja
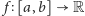 jest ciągła na
jest ciągła na
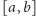 i ma
(powiedzmy ciągłą) pochodną w
i ma
(powiedzmy ciągłą) pochodną w
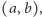 to mamy
to mamy
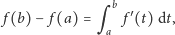 | (1) |
nie wolno opuścić założenia, iż pochodna istnieje w każdym punkcie
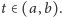 Nawet jeśli zbiór
Nawet jeśli zbiór
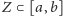 tych punktów,
gdzie
tych punktów,
gdzie
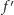 nie istnieje, jest bardzo mały – ma miarę Lebesgue’a
równą zero, tzn., intuicyjnie mówiąc, zerową długość – to może się
okazać, że funkcja
nie istnieje, jest bardzo mały – ma miarę Lebesgue’a
równą zero, tzn., intuicyjnie mówiąc, zerową długość – to może się
okazać, że funkcja
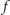 ciągła na
ciągła na
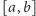 i różniczkowalna w
i różniczkowalna w
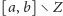 nie spełnia równości (1). Przykłady takich funkcji można
znaleźć we wspomnianym artykule; na marginesie naszkicowane są wykresy
dwóch: funkcji Cantora i Minkowskiego. Ta druga jest ciągła i ściśle
rosnąca na
nie spełnia równości (1). Przykłady takich funkcji można
znaleźć we wspomnianym artykule; na marginesie naszkicowane są wykresy
dwóch: funkcji Cantora i Minkowskiego. Ta druga jest ciągła i ściśle
rosnąca na
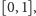 lecz jej pochodna nie ma ochoty być (choćby tu
i ówdzie) dodatnia, tylko znika prawie wszędzie. Jest prawie wszędzie taka, jaka
powinna być pochodna funkcji stałej, tylko że funkcja Minkowskiego stała,
niestety, nie jest.
lecz jej pochodna nie ma ochoty być (choćby tu
i ówdzie) dodatnia, tylko znika prawie wszędzie. Jest prawie wszędzie taka, jaka
powinna być pochodna funkcji stałej, tylko że funkcja Minkowskiego stała,
niestety, nie jest.
Kogoś, kto na studiach uczył się podstaw teorii miary i całki Lebesgue’a i wysłuchiwał, że zachowanie funkcji na zbiorze miary zero nie wpływa na wartość całki, takie przykłady z początku zwykle dziwią i lekko niepokoją. Nie ma jednak w nich żadnej sprzeczności. Po prostu, jeśli dobra, stara, klasycznie rozumiana pochodna nie wszędzie istnieje, to (czasem) nie koduje już informacji o przyrostach funkcji.
Można się z tym pogodzić i np. szukać coraz subtelniejszych, przeczących intuicji przykładów tego, że w twierdzeniu Newtona–Leibniza słówko prawie jest zakazane. Najważniejszą rzeczą, którą chciałbym Czytelnikowi powiedzieć, jest jednak to, że kontrprzykłady, choć ważne, są mimo wszystko drugorzędne, o ile nie służą dalszej budowie matematyki, tworzeniu takich dodatków do jej gmachu, które pozwalają – być może za pomocą zupełnie nowych pojęć, narzędzi i środków – robić coś, czego dotąd nie potrafiliśmy, albo wręcz uważaliśmy za niemożliwe. Nie chodzi wszak o to, żeby wszystko było zawsze po staremu.
Prawdziwie twórcze pytania, jakie stawiało sobie wielu matematyków między rokiem 1890 a 1940, gdy narodziły się i dojrzały teoria miary z analizą funkcjonalną, brzmią następująco:
Jak należałoby zmodyfikować lub rozszerzyć pojęcie pochodnej, żeby jakiś
odpowiednik równości (1) był prawdziwy także wtedy, gdy
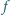 nie jest
różniczkowalna w każdym punkcie? Czy można będzie wtedy posługiwać
się innymi narzędziami rachunku całkowego, np. wzorem na całkowanie przez
części?
nie jest
różniczkowalna w każdym punkcie? Czy można będzie wtedy posługiwać
się innymi narzędziami rachunku całkowego, np. wzorem na całkowanie przez
części?
Okazuje się, że można to zrobić na kilka różnych, choć zasadniczo
równoważnych sposobów. Zacznijmy od takiego, który dla funkcji jednej
zmiennej jest naturalną drogą do uprawomocnienia wzoru Newtona–Leibniza (1)
dla odpowiednio zawężonej klasy funkcji ciągłych, różniczkowalnych
prawie wszędzie. Ustalmy przedział
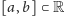 i funkcję całkowalną
i funkcję całkowalną
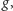 która za chwilę odegra rolę pochodnej innej funkcji. Niech
która za chwilę odegra rolę pochodnej innej funkcji. Niech
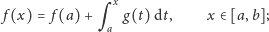 | (2) |
liczbę
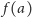 można wybrać dowolnie, a prawą stronę wzoru
traktujemy jako definicję
można wybrać dowolnie, a prawą stronę wzoru
traktujemy jako definicję
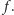 Nietrudno sprawdzić, że tak
określona funkcja
Nietrudno sprawdzić, że tak
określona funkcja
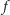 jest ciągła. To wynika z równości
jest ciągła. To wynika z równości
 a o ile całkujemy po dostatecznie
krótkim przedziale, to całka z funkcji całkowalnej jest mniejsza niż
dowolnie ustalony dodatni margines błędu, z upodobaniem oznaczany
literką
a o ile całkujemy po dostatecznie
krótkim przedziale, to całka z funkcji całkowalnej jest mniejsza niż
dowolnie ustalony dodatni margines błędu, z upodobaniem oznaczany
literką
 Subtelniejszą, ale wykonalną rzeczą jest wykazanie, że
Subtelniejszą, ale wykonalną rzeczą jest wykazanie, że
 ma pochodną
ma pochodną
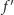 prawie wszędzie w
prawie wszędzie w
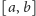 i w dodatku
i w dodatku
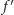 jest równa
jest równa
 też prawie wszędzie w
też prawie wszędzie w
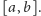
Te funkcje ciągłe, które otrzymuje się ze wzoru (2), zmieniając funkcję
całkowalną
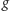 na wszelkie możliwe sposoby, nazywają się absolutnie
ciągłymi. To dla nich (i tylko dla nich) wzór Newtona–Leibniza ma sens;
można się nie obawiać, czy
na wszelkie możliwe sposoby, nazywają się absolutnie
ciągłymi. To dla nich (i tylko dla nich) wzór Newtona–Leibniza ma sens;
można się nie obawiać, czy
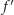 istnieje wszędzie, czy tylko prawie
wszędzie. Pozostałe funkcje ciągłe określa się mianem osobliwych. Słusznie; ich
miejsce jest w gabinecie osobliwości.
istnieje wszędzie, czy tylko prawie
wszędzie. Pozostałe funkcje ciągłe określa się mianem osobliwych. Słusznie; ich
miejsce jest w gabinecie osobliwości.
Równoważna definicja funkcji absolutnie ciągłych, nieco trudniejsza do
przełknięcia, ale lepiej poddająca się uogólnieniom na funkcje wielu zmiennych,
jest następująca. Przypuśćmy, że
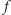 jest funkcją całkowalną na
przedziale
jest funkcją całkowalną na
przedziale
 Powiemy, że
Powiemy, że
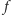 ma w
ma w
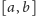 słabą
pochodną równą
słabą
pochodną równą
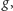 jeśli po pierwsze
jeśli po pierwsze
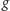 też jest całkowalna na
przedziale
też jest całkowalna na
przedziale
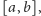 po drugie zaś wzór
po drugie zaś wzór
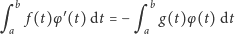 | (3) |
zachodzi dla każdej funkcji
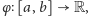 która ma ciągłą pochodną
i spełnia warunek
która ma ciągłą pochodną
i spełnia warunek
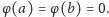
Cóż właściwie ma oznaczać taka, na pozór zupełnie niesprawdzalna,
definicja? Proszę myśleć o tym tak: gdyby
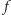 miała ciągłą
pochodną
miała ciągłą
pochodną
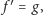 to dla każdej funkcji
to dla każdej funkcji
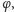 o której
mowa, mielibyśmy
o której
mowa, mielibyśmy
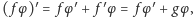 a ponadto
a ponadto
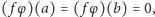 gdyż funkcja
gdyż funkcja
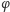 ma z założenia
znikać na końcach rozważanego przedziału. Zatem, na mocy wzoru
Newtona–Leibniza, całka z funkcji
ma z założenia
znikać na końcach rozważanego przedziału. Zatem, na mocy wzoru
Newtona–Leibniza, całka z funkcji
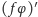 powinna być zerem,
a właśnie to jest przecież treścią wzoru (3). Mówiąc nieco inaczej, (3) to
wzór na całkowanie przez części, przemyślnie wbudowany w nową definicję
pojęcia pochodnej.
powinna być zerem,
a właśnie to jest przecież treścią wzoru (3). Mówiąc nieco inaczej, (3) to
wzór na całkowanie przez części, przemyślnie wbudowany w nową definicję
pojęcia pochodnej.
Co więcej, wzór (3) może zachodzić tylko dla jednej funkcji
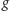 – gdyby
zachodził dla
– gdyby
zachodził dla
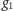 i
i
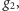 to odejmując dwie równości stronami,
otrzymalibyśmy
to odejmując dwie równości stronami,
otrzymalibyśmy
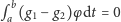 dla każdej
dla każdej
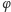 spełniającej
podane wcześniej warunki. Można wykazać – jest to tak zwany lemat du
Bois-Reymonda – że wtedy mamy
spełniającej
podane wcześniej warunki. Można wykazać – jest to tak zwany lemat du
Bois-Reymonda – że wtedy mamy
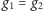 prawie wszędzie. Dlatego słaba
pochodna jest określona jednoznacznie, a jeśli przypadkiem
prawie wszędzie. Dlatego słaba
pochodna jest określona jednoznacznie, a jeśli przypadkiem
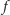 jest
ciągła i ma ciągłą pochodną określoną klasycznie, to obie pochodne są równe
(prawie wszędzie, rzecz jasna).
jest
ciągła i ma ciągłą pochodną określoną klasycznie, to obie pochodne są równe
(prawie wszędzie, rzecz jasna).
Można wykazać, że funkcja
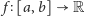 jest absolutnie ciągła,
tzn. jest całką
jest absolutnie ciągła,
tzn. jest całką
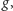 daną wzorem (2), wtedy i tylko wtedy, gdy
daną wzorem (2), wtedy i tylko wtedy, gdy
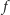 jest
całkowalna i ma całkowalną słabą pochodną. Obie drogi wyboru rodziny funkcji,
dla których (na każdym odcinku) zachodzi wzór Newtona–Leibniza, wiodą
zatem do tego samego celu.
jest
całkowalna i ma całkowalną słabą pochodną. Obie drogi wyboru rodziny funkcji,
dla których (na każdym odcinku) zachodzi wzór Newtona–Leibniza, wiodą
zatem do tego samego celu.
Po cóż komu takie pojęcia? Dlaczego studiować paskudne funkcje wielu zmiennych, których dziwacznie określone słabe pochodne są zaledwie funkcjami całkowalnymi, więc mogą np. okazać się nieciągłe w bardzo wielu punktach? Odpowiedzi, że przestrzenie takich funkcji – tzw. przestrzenie Sobolewa – są same w sobie ciekawymi obiektami badań, nie kupi wszak ani fizyk, ani niejeden matematyk. Prawdziwy sens i powód rozważania takich funkcji przynosi jednak teoria równań różniczkowych i jej pogranicze z fizyką oraz geometrią.
Dlaczego? Otóż, przestrzenie Sobolewa są dużo obszerniejsze od przestrzeni
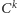 funkcji różniczkowalnych
funkcji różniczkowalnych
 -krotnie w sposób ciągły.
Pierwszym odruchem kogoś, kto próbuje dowodzić istnienia rozwiązań
równań różniczkowych, jest ograniczanie się właśnie do swojskich
i znanych funkcji klasy
-krotnie w sposób ciągły.
Pierwszym odruchem kogoś, kto próbuje dowodzić istnienia rozwiązań
równań różniczkowych, jest ograniczanie się właśnie do swojskich
i znanych funkcji klasy
 Postępując tak, wiążemy sobie ręce:
częścią dowodu istnienia musi być dowód ciągłości pochodnych.
Interpretując równanie w ogólniejszym języku przestrzeni Sobolewa,
otrzymujemy – po pierwsze – więcej kandydatur na rozwiązania, po drugie
zaś oddzielamy samą kwestię istnienia rozwiązania od sprawdzania jego
dodatkowych własności. Po trzecie, cała analiza funkcjonalna staje się skrzynią
z narzędziami, których w tym obszerniejszym świecie można używać.
Po czwarte, rozmaite zbiory funkcji, które w przestrzeniach
Postępując tak, wiążemy sobie ręce:
częścią dowodu istnienia musi być dowód ciągłości pochodnych.
Interpretując równanie w ogólniejszym języku przestrzeni Sobolewa,
otrzymujemy – po pierwsze – więcej kandydatur na rozwiązania, po drugie
zaś oddzielamy samą kwestię istnienia rozwiązania od sprawdzania jego
dodatkowych własności. Po trzecie, cała analiza funkcjonalna staje się skrzynią
z narzędziami, których w tym obszerniejszym świecie można używać.
Po czwarte, rozmaite zbiory funkcji, które w przestrzeniach
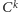 są
niezwarte, rozległe tak, że aż wiatr w nich hula, potrafią stawać się małe
i przytulne właśnie w przestrzeniach Sobolewa. Nabierają wtedy sensu proste
argumenty w rodzaju każda funkcja ciągła
są
niezwarte, rozległe tak, że aż wiatr w nich hula, potrafią stawać się małe
i przytulne właśnie w przestrzeniach Sobolewa. Nabierają wtedy sensu proste
argumenty w rodzaju każda funkcja ciągła
 na zbiorze zwartym
osiąga w pewnym punkcie swój kres dolny, często nieprzydatne, gdy
na zbiorze zwartym
osiąga w pewnym punkcie swój kres dolny, często nieprzydatne, gdy
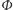 jest funkcjonałem na przestrzeni
jest funkcjonałem na przestrzeni
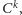 wyposażonej w nazbyt
wymagające pojęcie zbieżności. Po piąte wreszcie, bywa i tak, że nieliniowa
natura problemu sama wymusza istnienie osobliwości rozwiązań. Defekty
ciekłych kryształów, samoprzecięcia błon mydlanych... Wtedy przestrzenie,
dopuszczające nieciągłe rozwiązania, są jak znalazł.
wyposażonej w nazbyt
wymagające pojęcie zbieżności. Po piąte wreszcie, bywa i tak, że nieliniowa
natura problemu sama wymusza istnienie osobliwości rozwiązań. Defekty
ciekłych kryształów, samoprzecięcia błon mydlanych... Wtedy przestrzenie,
dopuszczające nieciągłe rozwiązania, są jak znalazł.
Pomysł, żeby znane pojęcie pochodnej zastąpić nowym, jest iście
szatański. Stefan Hildebrandt porównywał go do mefistofelesowskiego
wprowadzania papierowych pieniędzy zamiast złota. Papierowy oraz plastikowy
pieniądz, którego nośnik wart jest niewiele, ma jednak zalety; wygodniej
go nosić i przesyłać niż wory monet. Wygodniej dowodzić, że
się go ma. Kto zechce, może w bankomacie wymienić plastik na papier;
kto się uprze, dokona wymiany na złoto. Współczesna teoria równań
różniczkowych zna odpowiednik tego postępowania: używając misternie
splecionej sieci różnych nierówności, dowodzi się, że słabe rozwiązania
wielu równań są w istocie pięknymi, klasycznymi rozwiązaniami klasy
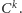
Bez pojęcia słabej pochodnej i masy jego konsekwencji cała armia moich starszych i młodszych kolegów po fachu byłaby częściowo bezrobotna. Nie byłoby też sporej części analizy funkcjonalnej i harmonicznej ani współczesnego matematycznego opisu chemotaksji, wirów w nadprzewodnikach, przejść fazowych, ruchu cieczy lepkich, dyfuzji w ośrodkach porowatych itp.
Warto więc w funkcjach Cantora i Minkowskiego, oraz im podobnych, widzieć nie tyle osobliwe kontrprzykłady, ale przede wszystkim drogowskazy, które pewnie były niewyraźne, ale, jak ze stuletniej perspektywy jasno widać, matematyków klasy Poincarégo, Hilberta, Weyla czy Sobolewa kierowały we właściwą stronę.
 i
i
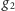 są ciągłe, dowód jest
łatwym zadaniem.
są ciągłe, dowód jest
łatwym zadaniem.
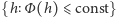 może być niezwarty w przestrzeni
może być niezwarty w przestrzeni
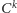 i zwarty w odpowiednio dobranej większej przestrzeni funkcyjnej,
z inną metryką, która sprawia, że zbiorów zwartych jest więcej.
i zwarty w odpowiednio dobranej większej przestrzeni funkcyjnej,
z inną metryką, która sprawia, że zbiorów zwartych jest więcej.