Czy naprawdę prawie robi wielką różnicę?
Jednym z fundamentalnych pojęć analizy matematycznej jest bez wątpienia różniczkowalność. Dla funkcji jednej zmiennej, określonej na pewnym otwartym przedziale, równoważna jest ona istnieniu pochodnej funkcji w każdym punkcie tego przedziału. Jak wiadomo, wszystkie funkcje elementarne są różniczkowalne w tym klasycznym sensie, jednak wiele innych prostych i zarazem użytecznych funkcji już nie.
Przykładem jest chociażby funkcja
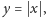 dla której wszystko psuje się
w zerze, w którym pochodna nie istnieje. Okazuje się jednak, że można tak
osłabić pojęcie różniczkowalności, że wyżej wspomniana funkcja
będzie już różniczkowalna w tym nowym sensie. Wystarczy w tym
celu wziąć pod uwagę tzw. różniczkowalność prawie wszędzie.
Cóż to oznacza? Pojęcie prawie wszędzie (będziemy też pisać p.w.)
jest krótszym określeniem na sformułowanie „wszędzie poza zbiorem
(jednowymiarowej) miary Lebesgue’a zero”. Wymyślona na początku
XX wieku przez Henri Lebesgue’a koncepcja miary, nazwanej później jego
nazwiskiem, jest niczym innym jak uogólnieniem pojęcia długości przedziału.
Dzięki tej mierze można jednak mierzyć dodatkowo „długości” wielu
innych zbiorów zawartych w prostej. Można np. zmierzyć „długość”
punktu (jego miara to zero), zbioru liczb naturalnych w
dla której wszystko psuje się
w zerze, w którym pochodna nie istnieje. Okazuje się jednak, że można tak
osłabić pojęcie różniczkowalności, że wyżej wspomniana funkcja
będzie już różniczkowalna w tym nowym sensie. Wystarczy w tym
celu wziąć pod uwagę tzw. różniczkowalność prawie wszędzie.
Cóż to oznacza? Pojęcie prawie wszędzie (będziemy też pisać p.w.)
jest krótszym określeniem na sformułowanie „wszędzie poza zbiorem
(jednowymiarowej) miary Lebesgue’a zero”. Wymyślona na początku
XX wieku przez Henri Lebesgue’a koncepcja miary, nazwanej później jego
nazwiskiem, jest niczym innym jak uogólnieniem pojęcia długości przedziału.
Dzięki tej mierze można jednak mierzyć dodatkowo „długości” wielu
innych zbiorów zawartych w prostej. Można np. zmierzyć „długość”
punktu (jego miara to zero), zbioru liczb naturalnych w
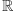 (miara
tego zbioru jest również równa zeru) lub „długość” zbioru liczb
niewymiernych w
(miara
tego zbioru jest również równa zeru) lub „długość” zbioru liczb
niewymiernych w
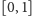 (miara w tym przypadku wynosi jeden).
Intuicyjnie czujemy, że jeżeli miara Lebesgue’a jakiegoś zbioru wynosi
(miara w tym przypadku wynosi jeden).
Intuicyjnie czujemy, że jeżeli miara Lebesgue’a jakiegoś zbioru wynosi
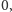 to musi on być „bardzo mały”. I choć dopuszczenie do sytuacji, że
funkcja nie musi być różniczkowalna na takim „małym” zbiorze,
wpłynie z pewnością na jej zachowanie i własności, to czy skutkiem tego
może być radykalna zmiana faktów znanych nam z klasycznej analizy
matematycznej?
to musi on być „bardzo mały”. I choć dopuszczenie do sytuacji, że
funkcja nie musi być różniczkowalna na takim „małym” zbiorze,
wpłynie z pewnością na jej zachowanie i własności, to czy skutkiem tego
może być radykalna zmiana faktów znanych nam z klasycznej analizy
matematycznej?
Aby odpowiedzieć na to pytanie, na początku odnotujmy następujące twierdzenie.
Twierdzenie 1. Jedyną
funkcją
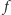 ciągłą w przedziale
ciągłą w przedziale
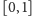 oraz spełniającą wszędzie
w przedziale
oraz spełniającą wszędzie
w przedziale
 warunek
warunek
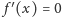 jest funkcja stała.
jest funkcja stała.
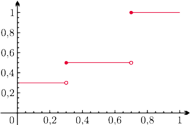
Rys. 1
Czy to twierdzenie pozostanie prawdziwe, gdy w miejsce słowa „wszędzie” wstawimy „prawie wszędzie”? Na pierwszy rzut oka wydaje się, że tak. Oczywiście, można z łatwością podać (patrz rysunek 1) przykład niemalejącej funkcji różniczkowalnej prawie wszędzie o pochodnej równej zeru, która nie jest stała, ale tę monotoniczność uzyskaliśmy za cenę nieciągłości funkcji. Czy jednak mimo wszystko mogą istnieć różne od stałej CIĄGŁE funkcje różniczkowalne p.w. o pochodnej równej zeru, które są, powiedzmy, niemalejące? I choć intuicja podpowiada, że takich obiektów matematycznych nie ma, to jak powiedział brytyjski matematyk Edward Titchmarsh „być może najbardziej zaskakujące w matematyce jest to, że jest tak zaskakująca”. Tak, są takie funkcje! Jedną z nich jest funkcja Cantora (zwana też funkcją Cantora–Lebesgue’a), pochodząca z 1883 roku. Do jej zdefiniowania będzie nam potrzebny tzw. zbiór Cantora. Przypomnijmy jego konstrukcję.
Zaczynamy od odcinka
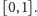 Dzielimy go na trzy podprzedziały równej
długości i środkowy z nich, otwarty, oznaczamy przez
Dzielimy go na trzy podprzedziały równej
długości i środkowy z nich, otwarty, oznaczamy przez
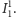 W kolejnym
kroku pozostałe dwa przedziały również dzielimy na trzy podprzedziały
każdy i środkowe z nich, otwarte, oznaczamy przez
W kolejnym
kroku pozostałe dwa przedziały również dzielimy na trzy podprzedziały
każdy i środkowe z nich, otwarte, oznaczamy przez
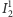 oraz
oraz
 W kolejnych krokach powtarzamy tę procedurę, tzn. po
W kolejnych krokach powtarzamy tę procedurę, tzn. po
 -tym kroku otrzymujemy
-tym kroku otrzymujemy
 przedziałów otwartych
przedziałów otwartych

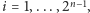 o długości
o długości
 każdy. Zbiór Cantora
określamy wówczas jako zbiór
każdy. Zbiór Cantora
określamy wówczas jako zbiór
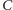 postaci
postaci

gdzie

Zbiór Cantora ma intrygujące własności. Przede wszystkim jest przykładem
domkniętego zbioru nieprzeliczalnego miary Lebesgue’a zero. Co więcej, należą
do niego tylko i wyłącznie te liczby z przedziału
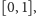 które da się
przedstawić w systemie trójkowym bez użycia
które da się
przedstawić w systemie trójkowym bez użycia
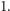
Oznaczmy teraz

Dla dowolnego naturalnego
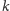 zdefiniujmy funkcję
zdefiniujmy funkcję
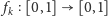 następująco:
następująco:

 oznacza domknięcie zbioru
oznacza domknięcie zbioru
 ), natomiast w domknięciach
przedziałów dopełniających zbiór
), natomiast w domknięciach
przedziałów dopełniających zbiór
 do przedziału
do przedziału
 określmy
funkcję
określmy
funkcję
 jako ciągłą i liniową, tak aby w całym przedziale
jako ciągłą i liniową, tak aby w całym przedziale
 funkcja
funkcja
 była ciągła. Funkcja
była ciągła. Funkcja
 będzie więc
niemalejąca i ciągła w
będzie więc
niemalejąca i ciągła w
 Co istotne, można wykazać, że ciąg
funkcyjny
Co istotne, można wykazać, że ciąg
funkcyjny
 jest jednostajnie zbieżny, a więc jego granica
jest jednostajnie zbieżny, a więc jego granica
 istnieje i jest funkcją ciągłą. Granicę tę nazywamy właśnie funkcją
Cantora. Jest ona niemalejąca (bo wszystkie
istnieje i jest funkcją ciągłą. Granicę tę nazywamy właśnie funkcją
Cantora. Jest ona niemalejąca (bo wszystkie
 są niemalejące) oraz stała
w każdym z przedziałów
są niemalejące) oraz stała
w każdym z przedziałów
 Stąd wynika od razu, że poza zbiorem
Cantora funkcja
Stąd wynika od razu, że poza zbiorem
Cantora funkcja
 ma pochodną równą
ma pochodną równą

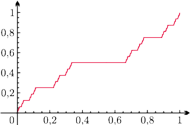
Rys. 2 Funkcja Cantora
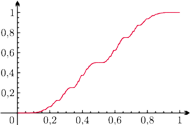
Rys. 3 Funkcja Minkowskiego
Widzimy więc, że istnieje funkcja ciągła, która jest określona na przedziale
długości
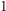 i której pochodna na zbiorze miary
i której pochodna na zbiorze miary
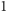 jest równa
jest równa
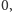 a mimo to nie jest funkcją stałą. Co więcej, przyjmuje wszystkie
wartości pomiędzy
a mimo to nie jest funkcją stałą. Co więcej, przyjmuje wszystkie
wartości pomiędzy
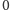 i
i
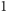 ! Zaiste, dziwna jest ta funkcja.
Zresztą czasami nazywa się ją również, ze względu na nieskończoną
ilość „schodków” (czyli tych fragmentów jej wykresu, na których jest
stała), „diabelskimi schodami”, co także podkreśla jej nieoczekiwane
własności. Z drugiej strony jednak, skoro istnieje taka funkcja jak funkcja
Cantora, to może warto zapytać, czy istnieje określona w przedziale
! Zaiste, dziwna jest ta funkcja.
Zresztą czasami nazywa się ją również, ze względu na nieskończoną
ilość „schodków” (czyli tych fragmentów jej wykresu, na których jest
stała), „diabelskimi schodami”, co także podkreśla jej nieoczekiwane
własności. Z drugiej strony jednak, skoro istnieje taka funkcja jak funkcja
Cantora, to może warto zapytać, czy istnieje określona w przedziale
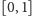 ŚCIŚLE monotoniczna funkcja CIĄGŁA, która prawie wszędzie
w
ŚCIŚLE monotoniczna funkcja CIĄGŁA, która prawie wszędzie
w
 będzie miała pochodną równą 0? I tu, co zaskakujące,
odpowiedź jest twierdząca! W literaturze znanych jest wiele funkcji o tej
własności (np. funkcje Riesza–Nagy’a), jednak tutaj podamy przykład
chyba najsłynniejszej wśród nich, a mianowicie funkcji Minkowskiego
będzie miała pochodną równą 0? I tu, co zaskakujące,
odpowiedź jest twierdząca! W literaturze znanych jest wiele funkcji o tej
własności (np. funkcje Riesza–Nagy’a), jednak tutaj podamy przykład
chyba najsłynniejszej wśród nich, a mianowicie funkcji Minkowskiego
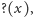 która po raz pierwszy na kartach historii matematyki pojawia się
w 1904 roku. Można ją określić na wiele sposobów. My do tego celu
wykorzystamy ułamki łańcuchowe. Przypomnijmy, że każdą liczbę
rzeczywistą
która po raz pierwszy na kartach historii matematyki pojawia się
w 1904 roku. Można ją określić na wiele sposobów. My do tego celu
wykorzystamy ułamki łańcuchowe. Przypomnijmy, że każdą liczbę
rzeczywistą
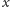 można przedstawić w postaci
można przedstawić w postaci

(przedstawienie to w skrócie można zapisać również jako
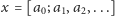 ), gdzie
), gdzie

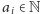 dla
dla
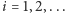 Co istotne, każda liczba niewymierna ma dokładnie jedno
takie przedstawienie (w postaci nieskończonego ułamka łańcuchowego),
dowolną zaś liczbę wymierną można zapisać w dwóch postaciach:
krótszej
Co istotne, każda liczba niewymierna ma dokładnie jedno
takie przedstawienie (w postaci nieskończonego ułamka łańcuchowego),
dowolną zaś liczbę wymierną można zapisać w dwóch postaciach:
krótszej
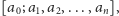 gdzie
gdzie
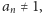 lub dłuższej
lub dłuższej
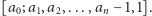 Oznaczmy
Oznaczmy
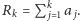 Wówczas na
przedziale
Wówczas na
przedziale
 funkcja Minkowskiego (zwana po angielsku question
mark) zdefiniowana jest następująco:
funkcja Minkowskiego (zwana po angielsku question
mark) zdefiniowana jest następująco:

Wykazanie, że
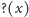 ma wymagane przez nas własności, czyli
ciągłość, ścisłą monotoniczność, pochodną prawie wszędzie równą
ma wymagane przez nas własności, czyli
ciągłość, ścisłą monotoniczność, pochodną prawie wszędzie równą
 jest o wiele trudniejsze niż w przypadku funkcji Cantora. Niemniej
jednak fakt istnienia takiej funkcji pozwala nam sformułować następujące
twierdzenie.
jest o wiele trudniejsze niż w przypadku funkcji Cantora. Niemniej
jednak fakt istnienia takiej funkcji pozwala nam sformułować następujące
twierdzenie.
Twierdzenie 2. Istnieją ściśle monotoniczne funkcje
ciągłe
 określone w przedziale
określone w przedziale
 oraz spełniające prawie
wszędzie w przedziale
oraz spełniające prawie
wszędzie w przedziale
 warunek
warunek
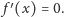
Jak widać, zmiana jakościowa między twierdzeniami 1 i 2 jest znaczna. Zatem także w matematyce prawie potrafi zrobić wielką różnicę...