Czy krowę można wpisać w kwadrat?
Jednym z najważniejszych pojęć matematycznych jest ciągłość. Założenie jej prowadzi do bardzo interesujących, a czasem nawet zaskakujących wniosków. Klasyczną własnością (zwaną własnością Darboux choć to nie Gaston Darboux jest jej autorem!) jest przyjmowanie wszystkich wartości pośrednich przez funkcję ciągłą na przedziale,oraz uogólnienia tego faktu. Konsekwencje tego mogą nas niejednokrotnie zaskoczyć.
Oto przykład: jakąkolwiek postać (np. krowę lub kota) narysuje dziecko na
kartce, zawsze można ją wpisać w kwadrat. Bardziej matematycznie: jeśli
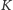 jest krzywą zamkniętą na płaszczyźnie, to na
jest krzywą zamkniętą na płaszczyźnie, to na
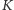 zawsze można
opisać kwadrat.
zawsze można
opisać kwadrat.
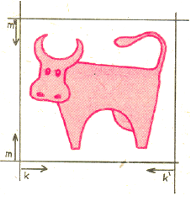
Rys. 1
Co to znaczy: wpisać krzywą w kwadrat lub – ogólniej – w prostokąt?
Wybierzmy dowolną linię prostą
 rozłączną z daną krzywą (Rys. 1)
i przesuwajmy ją prostopadle do jej kierunku, aż do momentu zetknięcia się
z krzywą. Następnie wybieramy taką prostą
rozłączną z daną krzywą (Rys. 1)
i przesuwajmy ją prostopadle do jej kierunku, aż do momentu zetknięcia się
z krzywą. Następnie wybieramy taką prostą
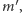 równoległą do
równoległą do
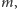 że krzywa leży między obiema prostymi i znów przesuwamy ją tak, by
zetknęła się z krzywą. Dalej wybieramy dwie proste
że krzywa leży między obiema prostymi i znów przesuwamy ją tak, by
zetknęła się z krzywą. Dalej wybieramy dwie proste
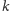 i
i
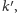 prostopadłe do
prostopadłe do
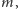 takie, by krzywa była zawarta między nimi,
a następnie powtarzamy operację jak w przypadku
takie, by krzywa była zawarta między nimi,
a następnie powtarzamy operację jak w przypadku
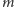 i
i
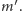 Otrzymane proste wyznaczają pewien prostokąt, w który krzywa będzie
wpisana.
Otrzymane proste wyznaczają pewien prostokąt, w który krzywa będzie
wpisana.
Krótko mówiąc, krzywa jest wpisana w prostokąt, gdy się w nim zawiera i z każdym z boków ma przynajmniej jeden punkt wspólny. Mając dany dowolny kierunek możemy skonstruować prostokąt, w który krzywa jest wpisana, i którego jeden z boków wyznacza tenże kierunek. Pokażemy, że zawsze można wybrać kierunek tak, by prostokąt ów był kwadratem.
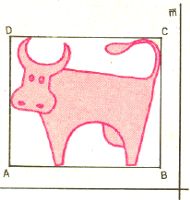
Rys. 2
Oznaczmy wierzchołki prostokąta przez
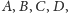 tak, by bok
tak, by bok
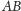 był równoległy do kierunku
był równoległy do kierunku
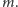 Przez
Przez
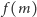 oznaczmy
długość boku
oznaczmy
długość boku
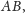 przez
przez
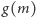 długość boku
długość boku
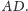 Niech
Niech
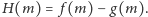 Prostokąt będzie kwadratem, gdy
Prostokąt będzie kwadratem, gdy
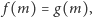 czyli
czyli
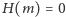 (Rys. 2).
(Rys. 2).
Zauważmy, że gdy
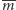 będzie prostą prostopadłą do
będzie prostą prostopadłą do
 i dla niej
przeprowadzimy odpowiednią konstrukcję prostokąta, to
i dla niej
przeprowadzimy odpowiednią konstrukcję prostokąta, to
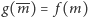 i
i
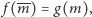 czyli
czyli

Rys. 3
Jeśli prostą
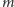 będziemy obracać (dookoła ustalonego na niej z góry
punktu), to nasz prostokąt będzie się zmieniać. Własności
będziemy obracać (dookoła ustalonego na niej z góry
punktu), to nasz prostokąt będzie się zmieniać. Własności
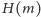 zależą w sposób ciągły od położenia prostej
zależą w sposób ciągły od położenia prostej
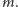 Z przedstawionych
wyżej własności wynika, że
Z przedstawionych
wyżej własności wynika, że
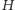 przyjmuje wartości różnych
znaków, musi więc przyjąć wartość zero. Stąd wnioskujemy, że istnieje taki
kierunek
przyjmuje wartości różnych
znaków, musi więc przyjąć wartość zero. Stąd wnioskujemy, że istnieje taki
kierunek
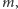 dla którego prostokąt opisany na krzywej
dla którego prostokąt opisany na krzywej
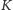 jest
kwadratem.
jest
kwadratem.
Można więc, na przykład, opisać kwadrat na rysunku krowy.
Przedstawione rozumowanie nie jest precyzyjnym dowodem, lecz jedynie jego
szkicem. Dokładnego określenia wymaga dziedzina funkcji
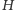 (korzystamy z własności Darboux, więc wypada mieć przedział – gdzie on
jest?). Należy formalnie uzasadnić, że funkcja
(korzystamy z własności Darboux, więc wypada mieć przedział – gdzie on
jest?). Należy formalnie uzasadnić, że funkcja
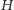 jest ciągła
…
jest ciągła
…
A co z pytaniem tytułowym? Mówiliśmy o rysunku krowy. Oryginalna krowa jest jednak tworem trójwymiarowym i należałoby się raczej pytać o możliwość jej wpisania w sześcian. Jeśli już stawiamy pytania, można się zastanowić, czy w krzywą zamkniętą da się wpisać kwadrat (a w przypadku trójwymiarowym – sześcian). W ten sposób można kontynuować badanie rozmaitych, niekiedy dosyć osobliwych, własności, u podstaw których leży pojęcie ciągłości.