Można sobie wyobrazić, że urządzenia obliczające pochodną czy całkę nie działają w sposób ciągły, lecz skokowo. Wówczas możemy odpowiednik pochodnej nazwać różnicą i zdefiniować jako

Bez trudu można przekonać się, że prawdziwe są następujące zależności

skąd – wobec oczywistego 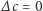dla dowolnej stałej  – mamy np.

Znający rachunek różniczkowy widzą, że wzory te są dokładnymi odpowiednikami wzorów dla pochodnej.

Z kolei odpowiednik całki będziemy nazywali antyróżnicą lub sumowaniem i oznaczali 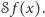 Zatem

I tutaj można wypisać wiele wzorów analogicznych do występujących w rachunku całkowym. Np. odpowiednik wynikającej ze wzorów wypisanych wyżej zależności

nazywany jest całkowaniem przez części – tu nazwiemy go sumowaniem przez części. Podobnie też, jak w rachunku całkowym, wprowadzimy sumowanie oznaczone 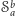określone przez warunek:

Poza zaciekawiającą analogią do pochodnych i całek wprowadzone pojęcia mają szereg interesujących zastosowań. Tu zajmiemy się jednym z nich – wykorzystamy je do obliczenia dla danego 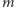 sumy dowolnie wielu -tych potęg kolejnych liczb naturalnych, poczynając od 1.

Do tego celu potrzebne nam będą tzw. liczby Stirlinga II rodzaju, które będziemy oznaczali 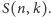Liczby te mówią, na ile sposobów można podzielić 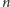-elementowy zbiór na 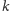 niepustych, rozłącznych podzbiorów. Liczby Stirlinga spełniają następującą zależność rekurencyjną:

Potrzebne nam też będą jeszcze pewne modyfikacje pojęcia potęgi. Potęgę kroczącą zdefiniujemy w następujący sposób:

Zauważmy, że

Okazuje się, że zróżnicowana potęga krocząca zachowuje się analogicznie do zróżniczkowanej zwykłej potęgi.

Warto odnotować, że

czego wygodniej nam będzie używać, gdy 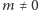zastąpimy przez

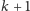
Wykorzystując definicję antyróżnicy, otrzymujemy wzór na sumowanie:

Musimy jeszcze zastanowić się, czy istnieje taka funkcja 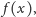  że

Łatwo można się zorientować, że jest nią

Zatem łącznie mamy (z dokładnością do stałej)

Wprowadziliśmy pojęcia potęgi kroczącej i liczb Stirlinga II rodzaju, ale jak to połączyć z obliczaniem sumy 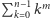? Okazuje się, że przydatne jest następujące twierdzenie

Dowód tego twierdzenia można przeprowadzić indukcyjnie, opierając się na wzorze rekurencyjnym na 

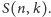
Teraz już obliczanie sumy potęg przebiega sprawnie. Oto przykład: kolejno obliczamy

I ostatecznie