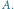Teoria stabilności w sensie Lapunowa i globalne atraktory
Jednym z głównych narzędzi służących do matematycznego opisu otaczającego nas świata są równania różniczkowe zwyczajne i cząstkowe.

W prostszych z nich, równaniach zwyczajnych, występuje pochodna szukanej
funkcji
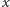 zmiennej rzeczywistej
zmiennej rzeczywistej
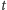 (mającej najczęściej interpretację
czasu). Ponieważ pochodna
(mającej najczęściej interpretację
czasu). Ponieważ pochodna
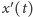 opisuje wzrost bądź malenie funkcji
opisuje wzrost bądź malenie funkcji
 w chwili
w chwili
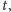 możemy uważać, że takie równania opisują
zmienność bądź ewolucję wielkości
możemy uważać, że takie równania opisują
zmienność bądź ewolucję wielkości
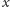 w czasie. Często zamiast
jednego równania różniczkowego zwyczajnego badamy cały układ takich
powiązanych ze sobą równań. Przykładem może tu być dobrze znany
z fizyki układ równań ruchu Newtona opisujący siłę
w czasie. Często zamiast
jednego równania różniczkowego zwyczajnego badamy cały układ takich
powiązanych ze sobą równań. Przykładem może tu być dobrze znany
z fizyki układ równań ruchu Newtona opisujący siłę
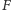 działającą
na ciało:
działającą
na ciało:

zapisany dla składowych wektora położenia
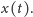 We wzorze powyżej
We wzorze powyżej
 jest masą ciała,
jest masą ciała,
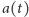 przyspieszeniem, zaś
przyspieszeniem, zaś
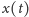 położeniem ciała w chwili
położeniem ciała w chwili
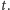 Symbol
Symbol
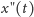 oznacza drugą
pochodną położenia względem czasu, czyli wektor przyspieszenia.
oznacza drugą
pochodną położenia względem czasu, czyli wektor przyspieszenia.
Ponieważ nie każde równanie różniczkowe zwyczajne (a tym bardziej
układ takich równań bądź równanie różniczkowe cząstkowe) potrafimy
jawnie rozwiązać (podać wzór analityczny na rozwiązanie
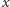 ),
matematycy zajmujący się badaniem tych równań stawiają zazwyczaj trzy
podstawowe pytania, na które starają się odpowiedzieć:
),
matematycy zajmujący się badaniem tych równań stawiają zazwyczaj trzy
podstawowe pytania, na które starają się odpowiedzieć:
- 1.
- Czy badane równanie ma rozwiązanie o określonych własnościach (np. ograniczone, różniczkowalne)? – istnienie rozwiązania.
- 2.
- Czy takie istniejące rozwiązanie (spełniające ew. pewne dodatkowe warunki) jest tylko jedno czy też może ich być więcej? – jednoznaczność rozwiązania.
- 3.
- Jakie dodatkowe własności ma rozwiązanie (np. czy będzie określone
dla wszystkich czasów
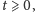 czy może w pewnej chwili
czy może w pewnej chwili
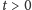 przestaje istnieć)? Jeśli rozwiązanie istnieje dla wszystkich
czasów
przestaje istnieć)? Jeśli rozwiązanie istnieje dla wszystkich
czasów
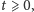 to czy potrafimy opisać sposób jego zachowania
po bardzo długim czasie? – zachowanie asymptotyczne.
to czy potrafimy opisać sposób jego zachowania
po bardzo długim czasie? – zachowanie asymptotyczne.
Pomyślmy tu o trzech przykładach równań różniczkowych zwyczajnych,
przy czym każde z tych równań rozpatrujemy z dodatkowym warunkiem
( warunkiem Cauchy’ego) zadającym wartość rozwiązania w chwili
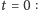

Łatwo przekonamy się, że rozwiązania tych równań dane są wzorami:

Możemy zauważyć, że rozwiązanie
 jest dobrze określone dla
czasów
jest dobrze określone dla
czasów
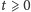 bliskich zera, lecz w chwili
bliskich zera, lecz w chwili
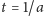 przestaje
istnieć. Rozwiązania
przestaje
istnieć. Rozwiązania
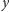 i
i
 istnieją natomiast dla wszystkich
istnieją natomiast dla wszystkich
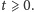 Można więc mówić o ich zachowaniu asymptotycznym,
gdy czas
Można więc mówić o ich zachowaniu asymptotycznym,
gdy czas
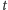 dąży do nieskończoności. Rozwiązanie
dąży do nieskończoności. Rozwiązanie
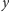 oscyluje okresowo, natomiast rozwiązanie
oscyluje okresowo, natomiast rozwiązanie
 dąży do 0, gdy czas
dąży do 0, gdy czas
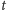 dąży do nieskończoności. Rozwiązanie
dąży do nieskończoności. Rozwiązanie
 ilustruje
sposób zachowania, który nawiązując do nazwiska prekursora badania
asymptotyki rozwiązań, określamy mianem asymptotycznej stabilności
w sensie Lapunowa (matematyk rosyjski A.M. Lapunow badał to pojęcie
już w 1892 roku). Uściślając naszą intuicję, sformułujmy następującą
definicję:
ilustruje
sposób zachowania, który nawiązując do nazwiska prekursora badania
asymptotyki rozwiązań, określamy mianem asymptotycznej stabilności
w sensie Lapunowa (matematyk rosyjski A.M. Lapunow badał to pojęcie
już w 1892 roku). Uściślając naszą intuicję, sformułujmy następującą
definicję:
Definicja. Powiemy, że rozwiązanie zerowe
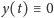 równania
różniczkowego zwyczajnego
równania
różniczkowego zwyczajnego
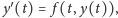 jest asymptotycznie
stabilne, jeżeli:
jest asymptotycznie
stabilne, jeżeli:
- 1.
- Dla dowolnego
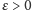 istnieje
istnieje
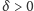 taka, że rozwiązania
odpowiadające warunkom początkowym spełniającym nierówność
taka, że rozwiązania
odpowiadające warunkom początkowym spełniającym nierówność
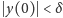 istnieją dla wszystkich czasów
istnieją dla wszystkich czasów
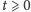 i spełniają
oszacowanie
i spełniają
oszacowanie
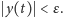
- 2.
- Rozwiązania dążą do zera, gdy czas
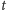 dąży
do nieskończoności.
dąży
do nieskończoności.
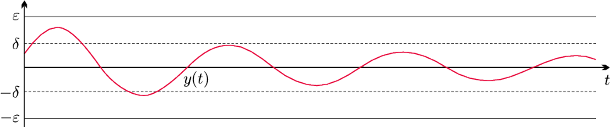
Definicję tę ilustruje następujący rysunek.
Jeśli badane równanie nie ma rozwiązania zerowego, ale pewne jego
rozwiązanie
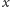 istnieje dla wszystkich czasów
istnieje dla wszystkich czasów
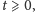 można
badać stabilność asymptotyczną rozwiązania
można
badać stabilność asymptotyczną rozwiązania
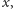 sprowadzając tę
bardziej złożoną sytuację do opisanego powyżej przypadku asymptotycznej
stabilności rozwiązania zerowego, rozpatrując różnicę
sprowadzając tę
bardziej złożoną sytuację do opisanego powyżej przypadku asymptotycznej
stabilności rozwiązania zerowego, rozpatrując różnicę
 gdzie
gdzie
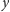 jest innym rozwiązaniem badanego równania.
jest innym rozwiązaniem badanego równania.
Idea stabilności asymptotycznej jest ważna z praktycznego punktu
widzenia. Otóż, jeżeli równanie różniczkowe opisuje pewien proces
fizyczny i rozwiązanie
 tego równania jest asymptotycznie stabilne, to
możemy uważać, że po dostatecznie długim czasie zaobserwujemy
praktycznie tylko wartości rozwiązań bardzo bliskie wartościom
tego równania jest asymptotycznie stabilne, to
możemy uważać, że po dostatecznie długim czasie zaobserwujemy
praktycznie tylko wartości rozwiązań bardzo bliskie wartościom
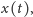 niezależnie od tego, z jakiego warunku początkowego zaczerpniętego ze zbioru
ograniczonego ten proces startował.
niezależnie od tego, z jakiego warunku początkowego zaczerpniętego ze zbioru
ograniczonego ten proces startował.
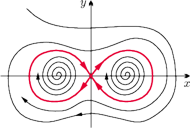
Kolorowa linia zamknięta jest właśnie zbiorem przyciągającym rozwiązania.
Szybki rozwój teoria stabilności rozwiązań równań różniczkowych przeżywała w drugiej połowie XX wieku. Trzeba tu wspomnieć nazwiska takich matematyków jak N.N. Krasowski, J.P. LaSalle, S. Lefschetz czy S. Yoshizawa. Pewnym niedostatkiem tej teorii jest jednak fakt, że zbiory, do których „przybliżają się” rozwiązania równań różniczkowych po długim czasie, są często bardziej złożone niż pojedynczy punkt (zerowe rozwiązanie równania). Popatrzmy na rysunek obok przedstawiający kształt zbioru przyciągającego dla prostego układu dwu równań różniczkowych na płaszczyźnie.
Zilustrowany powyżej przykład jest nadal znacznie prostszy od tych, które są
typowe w teorii równań różniczkowych cząstkowych. W każdej
chwili
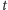 rozwiązanie takiego równania
rozwiązanie takiego równania
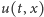 jest funkcją
zmiennej wektorowej
jest funkcją
zmiennej wektorowej
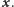 Zbiory, które przyciągają rozwiązania równań
cząstkowych, leżą w przestrzeni funkcji i mają często bardzo złożoną
strukturę. W ostatnich dwudziestu latach prowadzono intensywne badania
układów dyssypatywnych, tzn. takich układów fizycznych, w których
z upływem czasu następuje zanikanie bądź rozpraszanie energii (np. na skutek
tarcia). Przykładem może tu być, opisujące przepływ cieczy nieściśliwej,
równanie Naviera–Stokesa czy tzw. układy reakcyjno-dyfuzyjne modelujące
procesy biologiczne. Dla równań różniczkowych opisujących układy
dyssypatywne wprowadzono pojęcie globalnego atraktora. Jest to podzbiór
przestrzeni, w której zmieniają się rozwiązania ( przestrzeni fazowej), którego
obraz, jako całości, nie zmienia się w czasie ( zbiór niezmienniczy), zbiór ten
jest zwarty oraz przyciąga orbity wszystkich ograniczonych podzbiorów
przestrzeni fazowej.
Zbiory, które przyciągają rozwiązania równań
cząstkowych, leżą w przestrzeni funkcji i mają często bardzo złożoną
strukturę. W ostatnich dwudziestu latach prowadzono intensywne badania
układów dyssypatywnych, tzn. takich układów fizycznych, w których
z upływem czasu następuje zanikanie bądź rozpraszanie energii (np. na skutek
tarcia). Przykładem może tu być, opisujące przepływ cieczy nieściśliwej,
równanie Naviera–Stokesa czy tzw. układy reakcyjno-dyfuzyjne modelujące
procesy biologiczne. Dla równań różniczkowych opisujących układy
dyssypatywne wprowadzono pojęcie globalnego atraktora. Jest to podzbiór
przestrzeni, w której zmieniają się rozwiązania ( przestrzeni fazowej), którego
obraz, jako całości, nie zmienia się w czasie ( zbiór niezmienniczy), zbiór ten
jest zwarty oraz przyciąga orbity wszystkich ograniczonych podzbiorów
przestrzeni fazowej.
Badając równanie różniczkowe opisujące układ dyssypatywny, możemy
uważać, że jeżeli rozpatrzymy warunki początkowe należące do dowolnego
ograniczonego zbioru
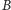 przestrzeni fazowej, to po skończonym czasie
odpowiadające im rozwiązania znajdą się w dowolnie małym otoczeniu
atraktora. Globalny atraktor, a raczej jego dowolnie małe otoczenie, jest więc tym
zbiorem, do którego każde rozwiązanie wpada po dostatecznie długim czasie i
pozostaje w jego obrębie już na zawsze. Często globalne atraktory są zbiorami
mającymi skończony wymiar topologiczny (tzn. można je utożsamiać
lokalnie z otwartym podzbiorem
przestrzeni fazowej, to po skończonym czasie
odpowiadające im rozwiązania znajdą się w dowolnie małym otoczeniu
atraktora. Globalny atraktor, a raczej jego dowolnie małe otoczenie, jest więc tym
zbiorem, do którego każde rozwiązanie wpada po dostatecznie długim czasie i
pozostaje w jego obrębie już na zawsze. Często globalne atraktory są zbiorami
mającymi skończony wymiar topologiczny (tzn. można je utożsamiać
lokalnie z otwartym podzbiorem
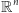 ). Jednak kształt atraktorów
wiążących się z fizycznymi układami dyssypatywnymi jest często bardzo
złożony, a same atraktory są fraktalami. Ewolucja w czasie obrazu
ograniczonego podzbioru
). Jednak kształt atraktorów
wiążących się z fizycznymi układami dyssypatywnymi jest często bardzo
złożony, a same atraktory są fraktalami. Ewolucja w czasie obrazu
ograniczonego podzbioru
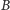 przestrzeni fazowej może wyglądać
następująco.
przestrzeni fazowej może wyglądać
następująco.

Po dostatecznie długim czasie rozwiązania rozpoczynające się w zbiorze
 wchodzą do
otoczenia globalnego atraktora
wchodzą do
otoczenia globalnego atraktora
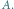
Do najbardziej znanych współczesnych matematyków badających teorię globalnych atraktorów należą: Jack K. Hale (USA), Roger Temam (Francja), A.V. Babin i M.I. Vishik (Rosja). Do dnia dzisiejszego powstają w ramach tej teorii nowe ciekawe rezultaty.
 wchodzą do
otoczenia globalnego atraktora
wchodzą do
otoczenia globalnego atraktora