Dlatego też – zamiast wymyślać kolejny sposób – postanowił uznać, że wszystkie funkcje to wielomiany – czasami bardzo wysokiego (żeby nie powiedzieć nieskończonego) stopnia (a więc również nieskończone szeregi potęgowe).

Aby teza taka dawała się stosować w praktyce, podał sposób zbudowania wielomianu, który w punktach 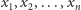przyjmuje odpowiednio wartości 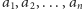. Oto ten wielomian

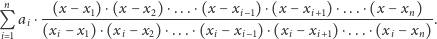
Mam nadzieję, iż Czytelnik bez trudu sprawdzi, że ten wielomian stopnia 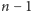rzeczywiście przyjmuje założone wartości, oraz sprawdzi, że wielomian niższego stopnia spełniający te warunki istnieje tylko dla specjalnego doboru wartości.

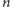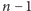Pomysł Lagrange’a – jak by powiedział Józef Szwejk – był dobry, ale głupi. Ten drugi epitet bierze się stąd, że jeśli poznalibyśmy wartość poszukiwanej funkcji-wielomianu w jeszcze jednym punkcie, to uzyskany w wyniku algorytmu Lagrange’a wielomian stopnia  miałby wykres w niczym nie przypominający swego poprzednika stopnia  . Dlatego też matematycy poszukiwali lepszego sposobu zastępowania dowolnych funkcji jakimiś prostymi szeregami. Największą karierę w drugiej połowie XIX wieku zrobiły szeregi trygonometryczne, a po następnych stu latach wymyślono już prawie doskonałe „zastępujące” trygonometrię falki. Ale to już inna historia.