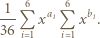Zadania z matematyki - XII 2020»Zadanie 1659
o zadaniu...
- Zadanie pochodzi z artykułu Zadania z matematyki - XII 2020
- Publikacja w Delcie: grudzień 2020
- Publikacja elektroniczna: 1 grudnia 2020
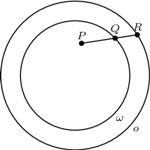
Dany jest basen w kształcie pierścienia kołowego, podzielony na 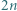 małych zbiorników poprzedzielanych zawieszonymi nad wodą obręczami
małych zbiorników poprzedzielanych zawieszonymi nad wodą obręczami 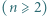 . W każdym małym zbiorniku (znajdującym się pomiędzy dwiema obręczami) pływa jeden delfin. Co jakiś czas dwa delfiny z sąsiednich zbiorników wykonują akrobację polegającą na jednoczesnym skoku przez obręcz (znajdującą się między zbiornikami) i w rezultacie - zamianie miejscami. Przypuśćmy, że po pewnym czasie każde dwa delfiny zamieniły się miejscami dokładnie raz. Wykazać, że pewna obręcz nie została użyta do wykonania żadnej akrobacji.
. W każdym małym zbiorniku (znajdującym się pomiędzy dwiema obręczami) pływa jeden delfin. Co jakiś czas dwa delfiny z sąsiednich zbiorników wykonują akrobację polegającą na jednoczesnym skoku przez obręcz (znajdującą się między zbiornikami) i w rezultacie - zamianie miejscami. Przypuśćmy, że po pewnym czasie każde dwa delfiny zamieniły się miejscami dokładnie raz. Wykazać, że pewna obręcz nie została użyta do wykonania żadnej akrobacji.
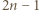

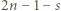
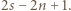



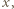
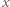
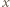
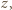

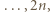
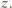

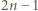

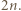
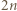
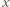
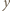
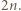

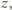
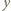 - jeszcze nie. Jednak po skoku przez obręcz między zbiornikami 1 i
- jeszcze nie. Jednak po skoku przez obręcz między zbiornikami 1 i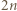
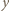


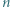
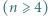 . Każda para osób rozegrała dokładnie jeden mecz, który zakończył się zwycięstwem jednej z
. Każda para osób rozegrała dokładnie jeden mecz, który zakończył się zwycięstwem jednej z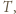
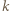
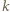 (krótko:
(krótko: 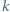 -cyklu).
-cyklu).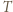
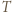
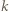 -cykl, to istnieje też
-cykl, to istnieje też 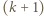 -cykl, dla
-cykl, dla 
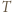
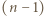 -cykl, czyli teza zadania.
-cykl, czyli teza zadania.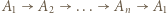
 -cyklem oraz niech
-cyklem oraz niech 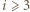
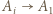 (zbiór takich indeksów jest niepusty, gdyż należy do niego
(zbiór takich indeksów jest niepusty, gdyż należy do niego  ). Wówczas
). Wówczas 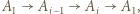
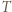
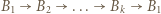
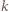 -cyklem, gdzie
-cyklem, gdzie 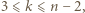
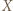
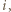
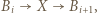
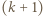 -cykl poprzez wstawienie
-cykl poprzez wstawienie 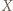
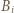
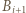 (przyjmujemy
(przyjmujemy 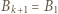 ). W
). W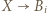
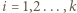
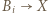
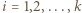 ; niech
; niech 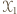
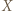
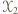 - zbiorem wierzchołków
- zbiorem wierzchołków 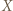
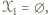
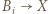
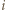
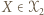 - nie mógłby wtedy jednak istnieć
- nie mógłby wtedy jednak istnieć 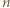 -cykl w
-cykl w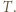
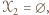
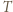
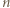 -cykl. Również gdyby
-cykl. Również gdyby 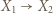
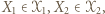
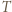
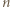 -cykl. Stąd wniosek, że istnieją wierzchołki
-cykl. Stąd wniosek, że istnieją wierzchołki 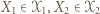
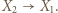
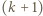 -cykl
-cykl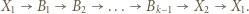
 -osobowych stołach usiadło
-osobowych stołach usiadło 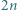
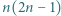
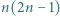
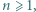
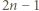
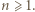
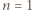
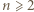
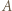
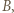
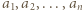
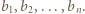
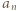
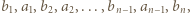
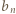
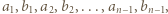
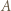
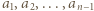
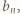
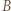
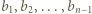
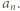
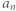
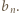
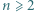
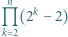
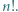
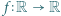
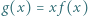
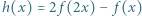
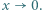
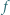
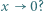
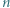
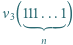
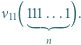
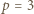 wystarczy rozważyć
wystarczy rozważyć 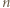 podzielne przez 3, a dla
podzielne przez 3, a dla 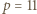 - rozważyć
- rozważyć  parzyste. Dla
parzyste. Dla 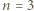 skorzystać z równości
skorzystać z równości 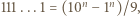 a dla
a dla 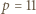 i
i 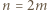 z równości
z równości 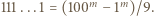
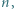
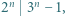
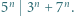
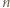 zachodzi nierówność
zachodzi nierówność 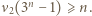 Wartość
Wartość 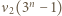 można wyznaczyć dokładnie, w zależności od parzystości
można wyznaczyć dokładnie, w zależności od parzystości 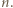 Skorzystać z nierówności
Skorzystać z nierówności 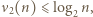 aby wykazać, że
aby wykazać, że 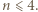
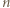 parzystych
parzystych 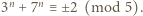 Dla
Dla 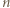 nieparzystych skorzystać z lematu w wersji z dodawaniem i postępować podobnie jak w podpunkcie (a).
nieparzystych skorzystać z lematu w wersji z dodawaniem i postępować podobnie jak w podpunkcie (a).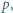
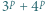
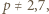 to
to 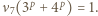
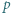 -adycznego w
-adycznego w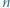
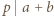 i
i 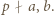 W przypadku
W przypadku 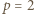 mamy
mamy 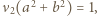 natomiast dla
natomiast dla 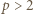 mamy
mamy 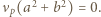
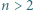
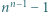
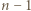 i stwierdzić, że
i stwierdzić, że 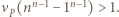

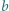
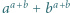
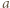 i
i 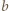 mają wspólny dzielnik pierwszy
mają wspólny dzielnik pierwszy 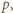 to
to 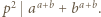 W przeciwnym razie istnieje liczba pierwsza
W przeciwnym razie istnieje liczba pierwsza 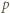 spełniająca warunki
spełniająca warunki 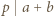 i
i 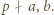 Wystarczy skorzystać z lematu w wersji z dodawaniem, rozumując podobnie jak w poprzednim zadaniu.
Wystarczy skorzystać z lematu w wersji z dodawaniem, rozumując podobnie jak w poprzednim zadaniu.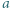
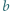
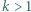
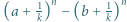
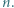
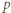 będzie dowolnym dzielnikiem pierwszym liczby
będzie dowolnym dzielnikiem pierwszym liczby 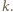 Jeśli liczba z zadania jest całkowita, to
Jeśli liczba z zadania jest całkowita, to 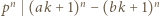 i można skorzystać z lematu, bo
i można skorzystać z lematu, bo 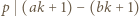 oraz
oraz 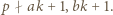
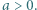
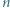
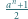
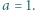
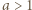 liczba
liczba 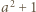 ma dzielnik pierwszy
ma dzielnik pierwszy 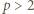 i dla odpowiednio dobranego nieparzystego
i dla odpowiednio dobranego nieparzystego 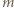 liczba
liczba 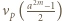 nie dzieli się przez 3.
nie dzieli się przez 3.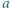
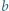
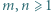
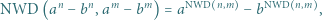
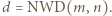 Stosując własności kongruencji, uzasadnić, że zbiór tych całkowitych
Stosując własności kongruencji, uzasadnić, że zbiór tych całkowitych 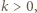 dla których
dla których 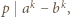 jest postaci
jest postaci 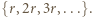
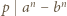 i
i 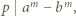 to
to 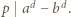
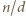 i
i 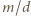
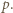 Wywnioskować z tego, że
Wywnioskować z tego, że 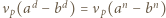 lub
lub 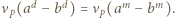
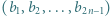
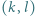
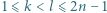
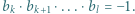
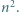
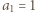
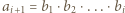
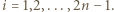
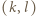
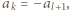
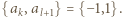
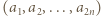
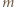
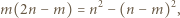
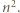
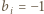
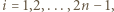
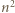
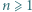
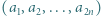
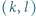
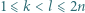
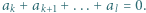
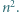
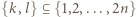
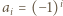
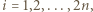
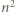
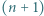 -poziomowego wieżowca, licząc z
-poziomowego wieżowca, licząc z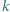 -tym piętrze, przy czym
-tym piętrze, przy czym 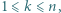
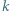
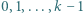
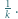

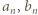
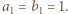

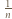
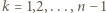
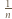
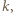
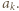
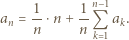
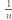
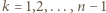
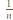
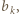
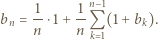
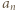
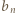
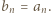
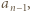
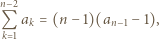
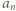
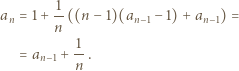
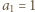
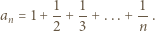
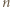 -ta suma częściowa szeregu harmonicznego, jest oczekiwaną liczbą cykli w
-ta suma częściowa szeregu harmonicznego, jest oczekiwaną liczbą cykli w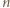 -elementowego. Jeśli ponadto ów Czytelnik należy do zbioru Czytelników Ambitnych, polecamy Mu znalezienie kombinatorycznego uzasadnienia tego związku.
-elementowego. Jeśli ponadto ów Czytelnik należy do zbioru Czytelników Ambitnych, polecamy Mu znalezienie kombinatorycznego uzasadnienia tego związku.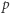 -adyczne
-adyczne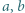
 :
:
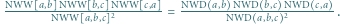
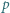
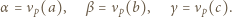
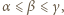
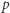 -adyczne
-adyczne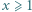
![|[x, 2x]](/math/temat/matematyka/teoria_liczb/zadania/2020/11/01/zm-20-11-kpo-2/2x-d7608384ddd380a3dd1f65eb0be5d8496d7a9363-im-2C,6B,73-FF,FF,FF.gif)
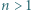 :
: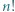
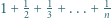
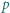
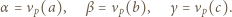
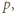
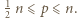
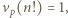
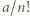
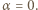
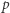 -adyczne
-adyczne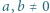
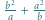
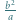
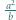
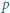
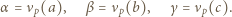
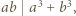
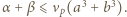
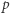 -adyczne
-adyczne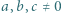
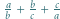
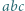
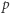 -adyczne
-adyczne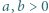
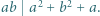

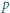
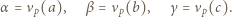
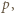
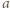
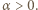

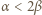
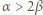
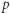 -adyczne
-adyczne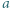
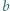
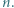
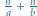
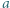
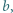
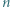
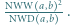
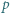
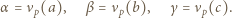
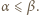
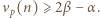
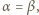
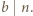
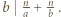
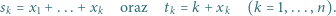
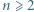
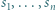

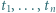
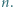
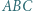
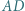
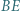
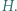
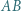
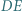
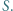
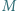
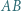
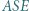
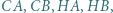
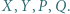
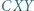
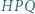
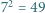
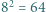
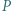
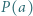
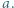
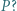

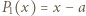
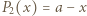
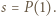
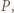
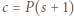 ; reprezentacja tej liczby w
; reprezentacja tej liczby w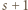

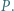
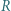
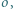
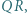
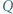
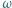
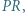

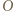
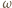
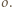
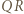
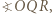
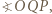
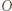
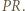
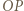
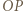
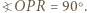
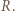
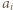
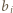
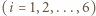 , to prawdopodobieństwo uzyskania sumy oczek równej
, to prawdopodobieństwo uzyskania sumy oczek równej