Delta mi!

Girard DESARGUES, matematyk, architekt ogrodów, doradca kardynała Richelieu (a więc rówieśnik Atosa, Portosa i Aramisa) postawił kolegom ogrodnikom pytanie: Jak posadzić 10 drzew w dziesięciu rzędach po 3 drzewa w każdym rzędzie?

Zasada Cavalieriego dla figur płaskich brzmi:
jeżeli dwie figury płaskie w przecięciu z każdą prostą równoległą do danej dają przekrój o tej samej długości, to pola tych figur są równe.

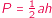
Najpopularniejszy wzór na pole trójkąta to jedna druga podstawa razy wysokość. Proste wnioski z tego wzoru pozwalają rozwiązać niełatwe czasem zadania.

Zdarza się czasem, że zachód słońca i pusta, piaszczysta plaża zachwycają nas, kiedy patrzymy na nie, spacerując brzegiem morza, jednak zamknięte w martwe ramy zdjęcia przywodzą na myśl co najwyżej słowo „kicz”. Ta historia, gdyby jeden z hollyłódzkich reżyserów zdecydował się nakręcić film na jej podstawie, wydałaby się z pewnością banalna. Tymczasem napisało ją życie.

W poprzednim deltoidzie zaprezentowano kilka zadań z geometrii płaskiej, rozwiązanych poprzez „wyjście w przestrzeń”. Oto garść kolejnych przykładów na to, że warto płaskie rysunki postrzegać jako ilustracje sytuacji trójwymiarowych.

Niektóre zadania z geometrii płaskiej łatwiej najpierw rozwiązać w przestrzeni, a później dopiero z powrotem je „spłaszczyć”. Liczne przykłady pojawiły się w  deltoidach 17 i 18. Oto jeszcze dwa tego rodzaju problemy.

W grudniu 2010 roku ukazał się drugi tom serii wydawniczej Biblioteczka Stowarzyszenia na rzecz Edukacji Matematycznej zatytułowany Matematyka. Poszukuję – odkrywam. Materiały w nim zawarte stanowią opracowania referatów wygłoszonych w ramach konferencji Konkursy matematyczne w Polsce, zorganizowanej w 2008 roku przez Uniwersytet Warszawski we współpracy ze Stowarzyszeniem na rzecz Edukacji Matematycznej.

Myślę, że niemal każdy Czytelnik miał okazję się z nią spotkać. Załóżmy, że mamy dany trójkąt, i wybierzmy dowolny punkt  z okręgu na nim opisanego. Wówczas rzuty prostokątne punktu  na proste zawierające boki danego trójkąta leżą na jednej prostej zwanej prostą Simsona.

13 i 14 kwietnia odbyły się zawody finałowe LXII OLimpiady Matematycznej. Każdego dnia zawodów 139 uczniów z całej Polski, przez trzysta minut, rozwiązywało trzy zadania. Wszystkie bezbłędnie rozwiązał Filip Borowiec z Kielc, a Maciej Dulęba z Wrocławia i Damian Orlef z Zabrza rozwiązali po pięć i pół.

Niektóre sumy nieskończone można zilustrować, tworząc nieskończony rysunek, którego pewna część jest podobna do całości. Na przykład na rysunku taką częścią jest jego prawa górna ćwiartka, a także prawa górna ćwiartka tej ćwiartki itd.

W dniu  marca 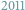 roku w budynku Szkoły Przymierza Rodzin w Warszawie przy ulicy Grzegorzewskiej  odbył się finał VI Olimpiady Matematycznej Gimnazjalistów. W czasie trzech godzin uczestnicy zawodów zmagali się z pięcioma zadaniami finałowymi, z których jedno (naszym zdaniem najtrudniejsze) omawiamy poniżej.

W zawodach II stopnia LXII Olimpiady Matematycznej wzięło udział 599 uczniów z całej Polski. Spośród nich do finału zakwalifikowano 139 osób.

Richard Feynman, laureat Nagrody Nobla z fizyki, miał bardzo krytyczny stosunek do rozważań czysto teoretycznych. Wspomina o tym Kai Lai Chung, wybitny probabilista amerykański, w książce Green, Brown and Probability.

Obrazem anamorficznym nazywamy obraz powstały przez celowe zniekształcenie jego proporcji w taki sposób, aby jego poprawny odczyt był możliwy przez popatrzenie na niego z ustalonej perspektywy lub odbicie go w odpowiednim zwierciadle.

Ktoś mi kiedyś powiedział o zadaniach geometrycznych: Jeśli nie wiesz, co zrobić, narysuj równoległobok! Jakkolwiek żartobliwa i niepoważna może się ta porada wydawać, jednak czasem działa. Oto kilka przykładów.

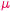
Tematem mojej pracy były własności pewnych szczególnych punktów na płaszczyźnie – punktów tytułowego zbioru W poniższym tekście przedstawię niektóre z tych własności oraz przykłady pokazujące, że przy użyciu dowiedzionych twierdzeń można wyciągnąć wiele niemal natychmiastowych wniosków.

W wielu zadaniach dane są trzy punkty, które albo są współliniowe, albo należy to o nich udowodnić. Wygodnym narzędziem bywa wtedy Twierdzenie Menelaosa.

W roku szkolnym 2010/2011 Stowarzyszenie na rzecz Edukacji Matematycznej jest organizatorem LXII edycji Olimpiady Matematycznej. Od września do grudnia roku uczestnicy Olimpiady Matematycznej zmagali się z dwunastoma zadaniami domowymi pierwszego etapu zawodów

Pomysł tego artykułu powstał na lekcji matematyki w I klasie gimnazjum. Rozwiązywałem z uczniami zadanie z podręcznika wydanego przez Gdańskie Wydawnictwo Oświatowe: który z narysowanych trójkątów jest przystający do trójkąta ?
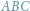