Delta mi!

Czy dwa identyczne rysunki mogą się przydać w jednym zadaniu? Mogą, na przykład gdy drugi jest obrazem pierwszego po pewnej, sprytnie dobranej inwersji...

Na zawodach II stopnia VIII OMG, które odbyły się 5 stycznia 2013, jedno z zadań było następujące...

Tym razem o inwersji – przekształceniu określanym czasem jako symetria względem okręgu.

Geometria analityczna kojarzona bywa z dużą ilością rachunków, takie rozwiązania często są długie i pracochłonne. Oto kilka przykładów, że nie zawsze jest tak źle.

W podróży bardzo istotną rolę odgrywa mapa, na której określa się i zaznacza aktualną pozycję, rozmaite odległości (np. odległość przebytą, do mijanych obiektów, pozostałą do celu podróży) oraz kąty (np. kursy, namiary).

Gdzie na płaszczyźnie znajdują się punkty, których stosunek odległości do dwóch ustalonych punktów 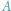 i 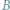 równy jest danej dodatniej stałej

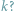
Matematycy od wielu lat zajmują się wędrówką po okręgu. Jednym z najbardziej znanych przykładów jest chyba skakanie po nim w określonym kierunku tak, by między kolejnymi punktami, w których się znajdziemy, była określona odległość  (mierzona wzdłuż łuku). Naturalne staje się wówczas pytanie, czy skacząc tak po okręgu, wrócimy kiedykolwiek do punktu wyjścia (widać, że rozwiązanie problemu nie zależy od punktu startowego)? Odpowiedź nasuwa się prędko – powrót nastąpi tylko wówczas, gdy stosunek długości okręgu do liczby  jest liczbą wymierną. Spróbujmy tym razem powędrować w inny sposób, określony geometrycznie.

Ortocentrum trójkąta to punkt przecięcia jego wysokości. Przyjmijmy oznaczenia jak na rysunkach 1 i 2 oraz założenie, że trójkąt  jest ostrokątny.

Trzy niewspółliniowe punkty na płaszczyźnie jednoznacznie wyznaczają okrąg, który przez nie przechodzi. Zatem jeśli pewne cztery punkty leżą na jednym okręgu, to jest to fakt godny odnotowania. W geometrii istnieje niezwykle urocze twierdzenie, które mówi, że aż dziewięć szczególnych punktów trójkąta leży na jednym okręgu.

Oczywiście, V postulatu Euklidesa nie da się dowieść na podstawie poprzednich czterech. Niemniej jednak praktycznie każdy znaczący matematyk od V do XIX wieku taki dowód przeprowadził i dopiero jego koledzy wskazywali, w którym miejscu rozumowania użył przesłanki z czterech początkowych postulatów niewynikającej...

Połączenie matematyki z religią może wydawać się nam, Europejczykom, dość zaskakujące. W Japonii jednak przez bardzo długi czas nie było niczym niezwykłym. Zjawisko to zostało zapoczątkowane w XVII wieku, kiedy władcy tego kraju podjęli decyzję o zamknięciu portów i odcięciu Japonii od reszty świata, szczególnie od Europy Zachodniej, a trwało do XIX wieku.

Od dwóch lat Fundacja Matematyków Wrocławskich oraz Instytut Matematyczny Uniwersytetu Wrocławskiego organizują konkurs matematycznego origami „Żuraw”. Mogą w nim startować uczniowie ze wszystkich typów szkół, a także dorośli amatorzy i profesjonalni matematycy. W odróżnieniu od innych konkursów origami w tym nie wystarczą zdolności manualne. W eliminacjach zawodnicy wykonują model matematyczny (płaski lub przestrzenny) w technice origami, natomiast w finale jest na odwrót – rozwiązują problemy dotyczące sztuki origami, używając technik matematycznych.

Poprzedni deltoid poświęcony był osiom potęgowym, między innymi twierdzeniu, które w skrócie brzmi tak: osie potęgowe trzech okręgów przecinają się w jednym punkcie. Ciekawym jego zastosowaniem jest dowód twierdzenia Brianchona.

7 stycznia 2012 roku około 1400 uczniów wzięło udział w drugim etapie VI Olimpiady Matematycznej Gimnazjalistów. Najciekawszym i jednocześnie najtrudniejszym zadaniem okazało się zadanie z planimetrii oznaczone numerem 5. Rozwiązało je niewielu uczniów, przy czym żaden z nich nie rozważył wszystkich możliwych konfiguracji. Poniżej postaramy się zadanie to dokładnie zanalizować.

Nieco więcej o potędze punktu względem okręgu.

W Delcie 6/2011 Jerzy Zabczyk przytoczył anegdotę o Feynmanie w związku z pewnym geometrycznym zadaniem efektownie umieszczonym przez Hugona Steinhausa w Kalejdoskopie matematycznym (o czym Feynman nie wiedział) i zaproponował Czytelnikom atrakcyjne zadania.