
Problem przesunięcia sofy
Jakie jest maksymalne pole sofy, którą można przesunąć przez korytarz w kształcie litery L o jednostkowej szerokości? - taki problem sformułował ponad 50 lat temu austriacko-kanadyjski matematyk Leo Moser.

Jakie jest maksymalne pole sofy, którą można przesunąć przez korytarz w kształcie litery L o jednostkowej szerokości? - taki problem sformułował ponad 50 lat temu austriacko-kanadyjski matematyk Leo Moser.

Rys. 1
W Delcie 11/2017 został przedstawiony (bez dowodu) fakt, że dla czterech dowolnych prostych (tak dowolnych, że są parami nierównoległe i żadne trzy nie mają punktu wspólnego) ortocentra wyznaczonych przez nie czterech trójkątów leżą na jednej prostej, a okręgi opisane na tych trójkątach mają punkt wspólny. Ponadto parabola, której kierownicą jest prosta zawierająca ortocentra, a ogniskiem punkt wspólny okręgów opisanych jest styczna do czterech wyjściowych prostych (Rys. 1).
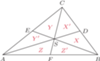
Punkty D, E, F to środki boków, X, X', Y, Y', Z, Z' oznaczają pola.
Środkowa trójkąta to odcinek łączący wierzchołek ze środkiem przeciwległego boku. Środkowe przecinają się w jednym punkcie, zwanym środkiem ciężkości i dzieli on każdą z nich w stosunku 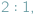 licząc od wierzchołka trójkąta (rys. obok).
licząc od wierzchołka trójkąta (rys. obok).
Tym razem o paraboli...
"Nie będziemy gadać niepotrzebnych rzeczy."
St.I. Witkiewicz, Szewcy, 1934
Wysokością czworokąta nazwijmy prostą przechodzącą przez środek jego boku i prostopadłą do boku przeciwległego. W niektórych czworokątach wszystkie cztery wysokości przecinają się w jednym punkcie - ortocentrum czworokąta. Przykładowo kwadrat ma ortocentrum, a romb niebędący kwadratem nie ma.
W wielu zadaniach, w których występują kąty lub ich sumy, przydatne bywa przeniesienie pewnych figur tak, by kąty te znalazły się obok siebie. Szczególnie wygodne jest to wtedy, gdy suma pewnych kątów równa jest np. 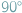 lub
lub 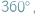 a także, gdy niektóre z danych odcinków są równej długości.
a także, gdy niektóre z danych odcinków są równej długości.
Geometrzy od dawna marzyli o współrzędnych jednorodnych, czyli takich 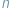 -tkach liczb (dalej dla uproszczenia będzie mowa o parach i trójkach) przyporządkowanych punktom, że gdy wszystkie liczby w
-tkach liczb (dalej dla uproszczenia będzie mowa o parach i trójkach) przyporządkowanych punktom, że gdy wszystkie liczby w 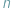 -tce pomnożymy przez tę samą liczbę, to nowa
-tce pomnożymy przez tę samą liczbę, to nowa 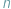 -tka będzie współrzędnymi tego samego punktu.
-tka będzie współrzędnymi tego samego punktu.
W tym artykule omówimy pewną bardzo pożyteczną technikę - tzw. przesuwanie. Polega ona na tym, że niektóre obiekty przesuwamy o pewien wektor i udowadniamy, że teza zadania jest niezmiennicza ze względu na wykonanie tej operacji. Ta metoda pozwala na sprowadzenie rozwiązywanego zadania do znacznie prostszego. Bardzo często ten prostszy przypadek ma jakiś rodzaj symetrii, z której łatwo wywnioskować tezę. Zanim przejdziemy do rozwiązywania zadań, odnotujmy dwie proste własności opisanej operacji.
Dawno, dawno temu żył sobie beztrosko król wraz ze swoją piękną córką. Jak to czasem w zbyt szczęśliwych królestwach bywa, pewnego razu czarnoksiężnik przybył na dwór, żeby porwać królewnę i uwięzić ją w swojej upiornej wieży. Zgodnie z zasadami dobrego wychowania mrocznych czarodziei, do których należał, musiał dać mieszkańcom królestwa możliwość ocalenia królewny przed swoim niecnym planem...
Tzw. zagadnienie Fermata to pytanie o to, gdzie wewnątrz danego trójkąta 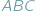 należy umieścić punkt
należy umieścić punkt 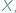 aby suma długości odcinków
aby suma długości odcinków 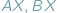 i
i 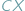 przyjęła najmniejszą wartość.
przyjęła najmniejszą wartość.
W geometrii dyskretnej przyjęło się mówić, że wielokąt jest wpisany w inny wielokąt, gdy ma wierzchołki na prostych zawierających boki tego drugiego wielokąta. Od czasu Hilberta tego zwrotu używa się i w przypadku "zwyczajnej" geometrii.
...z których żadne dwie nie są równoległe, a żadne trzy nie mają punktu wspólnego... tworzą cztery trójkąty - to każdy widzi i nikt się nie dziwi.
Planimetria Stowarzyszenie na rzecz Edukacji Matematycznej
W LXVIII Olimpiadzie Matematycznej uczestniczyło 1495 uczniów, zatem o 324 osoby więcej niż rok wcześniej, do zawodów stopnia drugiego zakwalifikowano 632 uczniów, a do zawodów stopnia trzeciego - 154 uczniów. Zapewne wynika to z pojawienia się w pierwszym stopniu sporej liczby zadań stosunkowo łatwych, a już na pewno niewymagających szczególnego przygotowania...

Rys. 1
Odcinek 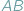 widać z punktu
widać z punktu 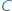 pod kątem
pod kątem 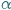 , gdy
, gdy 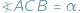 Z twierdzenia o kątach wpisanych wynika, że jeśli punkty
Z twierdzenia o kątach wpisanych wynika, że jeśli punkty 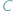 i
i 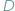 leżą na okręgu po tej samej stronie jego cięciwy
leżą na okręgu po tej samej stronie jego cięciwy 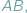 to widać ją z
to widać ją z 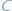 i
i 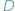 pod tym samym kątem (Rys. 1).
pod tym samym kątem (Rys. 1).

Rys. 1
Każdy zna twierdzenie o kącie zewnętrznym trójkąta: jest on równy sumie kątów wewnętrznych do niego nie przyległych (Rys. 1), co bierze się z faktu, że suma kątów przyległych jest równa sumie kątów trójkąta. Z twierdzenia tego wynika nietrudno twierdzenie o kącie wpisanym i środkowym: kąt wpisany jest równy 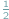 kąta środkowego opartego na tym samym łuku.
kąta środkowego opartego na tym samym łuku.

Fakt (*). W trójkącie prostokątnym środek przeciwprostokątnej jest równo odległy od wierzchołków. Również na odwrót, jeśli środek okręgu opisanego leży na boku trójkąta, to trójkąt ten jest prostokątny.